终于到了最关键的环节,也是最难的环节,如何求出开关级的传递函数?
也就是下图这一级。
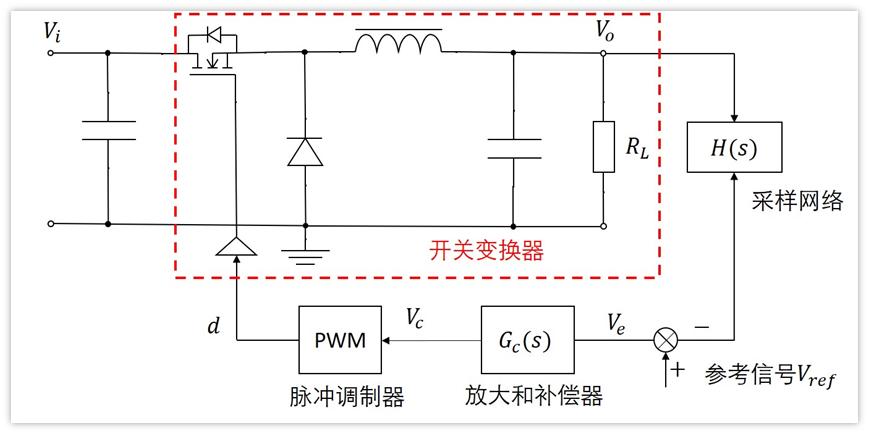
哎,不得不说,太难了。。。
不过没办法,先前夸下海口,跟兄弟们说我要把环路搞清楚,现在搞不动也得搞啊。

这一级之所以这么难,主要是有开关元器件,本身是非线性的。
当然了,前面第2小节我们已经阐明了,在满足低频,小信号等条件下,也可以看成是线性的,这里就不再说了。
那么如何求解传递函数呢?
求解方法
求的方法有很多种,常见的有下面这几种:
1、小信号模型的建模思路——基本建模法
2、状态空间平均法
3、开关元件平均模型法
4、开关网络平均模型法
上面这几种方法在《开关变换器的建模与控制+张卫平编著》这本书中都有非常专业详细的讲解。其实我此章也主要是看这本书进行的一个总结。
我个人觉得最好的应该是第4种——开关网络平均模型法,或者说这是我最喜欢的方法吧,也是我深入去看的一种方法。
不过原书中的方法会画出有变压器的等效电路,我不喜欢引入变压器,所以我下面介绍的过程是没有引入变压器的,直接推导出的公式。
Buck的CCM模式求解过程
求解过程主要有这么几步:
1、二端口等效
2、端口参数关系,推导出两个式子
3、代入电路,结合原理推导出传递函数
二端口等效
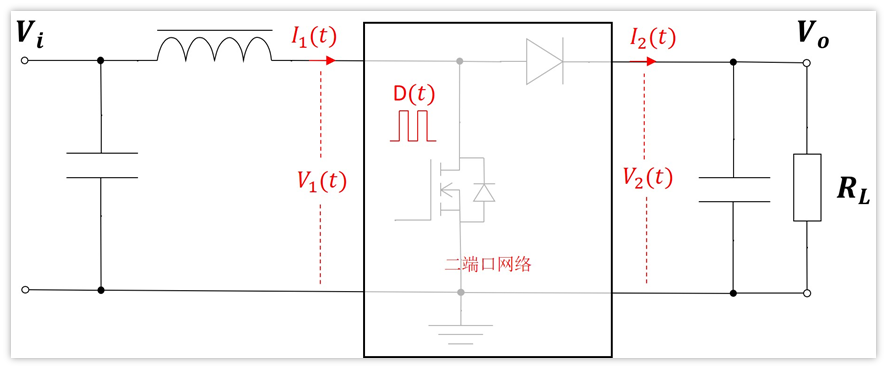
先来看二端口等效是怎么回事,下面是buck的拓扑。
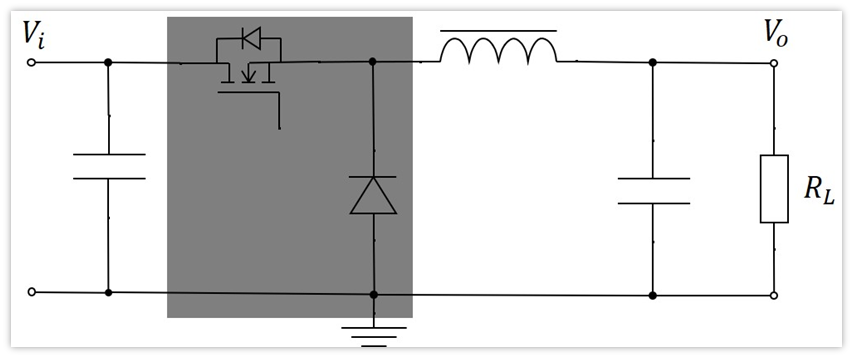
最难搞的就是里面这个MOS管和二极管了,那咋整呢?
干脆就把它看作一个整体,对外有四根线,同时底下两根线接地,所以也就是说有两个端口,是一个二端口网络。
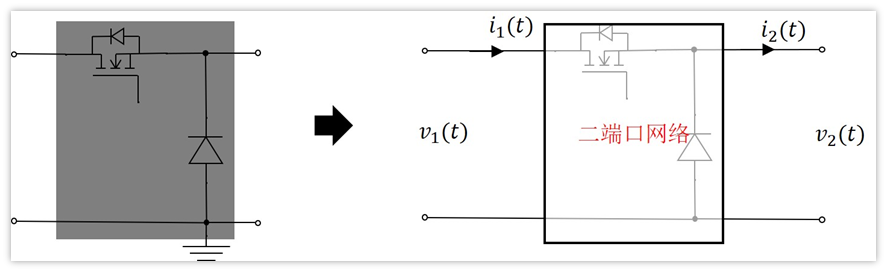
那么电路变成下面这样的了
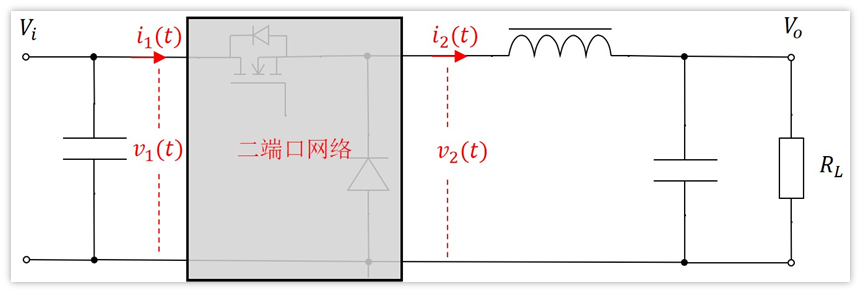
按照上图一等效,好像也没什么卵用,反而更加不熟悉了。先不着急
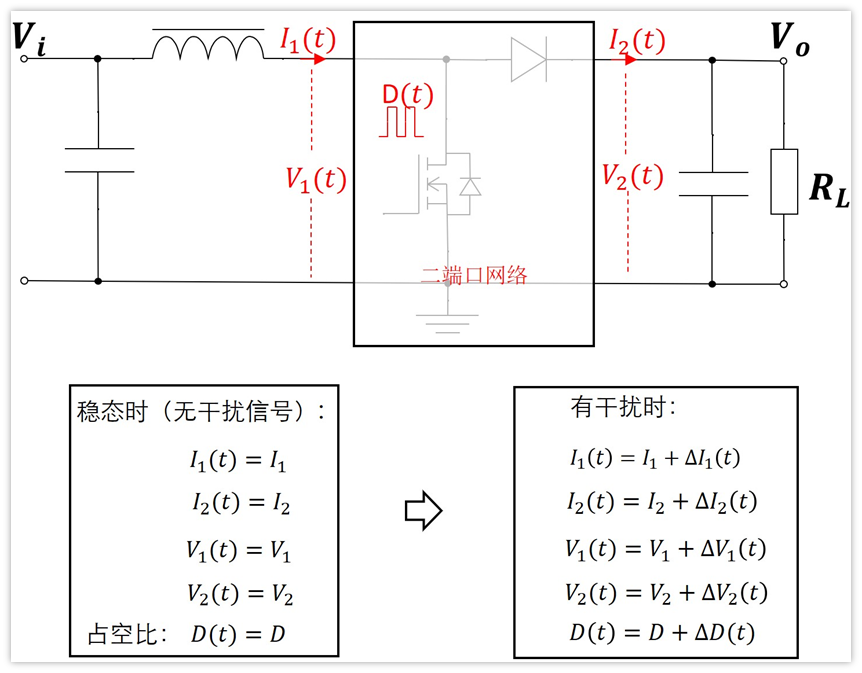
我们需要先对i1(t),i2(t),v1(t),v2(t)取开关周期的平均值,注意,是开关周期平均值,而不是总时间平均值。因为如果是总时间的平均值,那就只是直流等效了。
这里多一嘴,说说开关周期平均值和总时间平均值有什么差别,因为我在这里想了比较久,并且看起来两个值好像是一样的。
确实,如果是稳态,没有干扰信号,负载恒定,上述变量在每一个开关周期内的平均值都是一样的,并且等于总时间的平均值。
但是如果有干扰信号,那么可能上一个周期的平均值跟下一个周期的平均值不一样,也就是它是时间的函数。我们现在分析传递函数,就是分析干扰信号的影响,自然不能只看直流等效了,所以求的是开关周期的平均值。
那问题来了?求开关周期的平均值合理吗?
其实这里就有用到前面所说的线性化条件——低频信号假设,我们研究的信号大大低于开关频率,因此求开关周期的平均值是合理的。
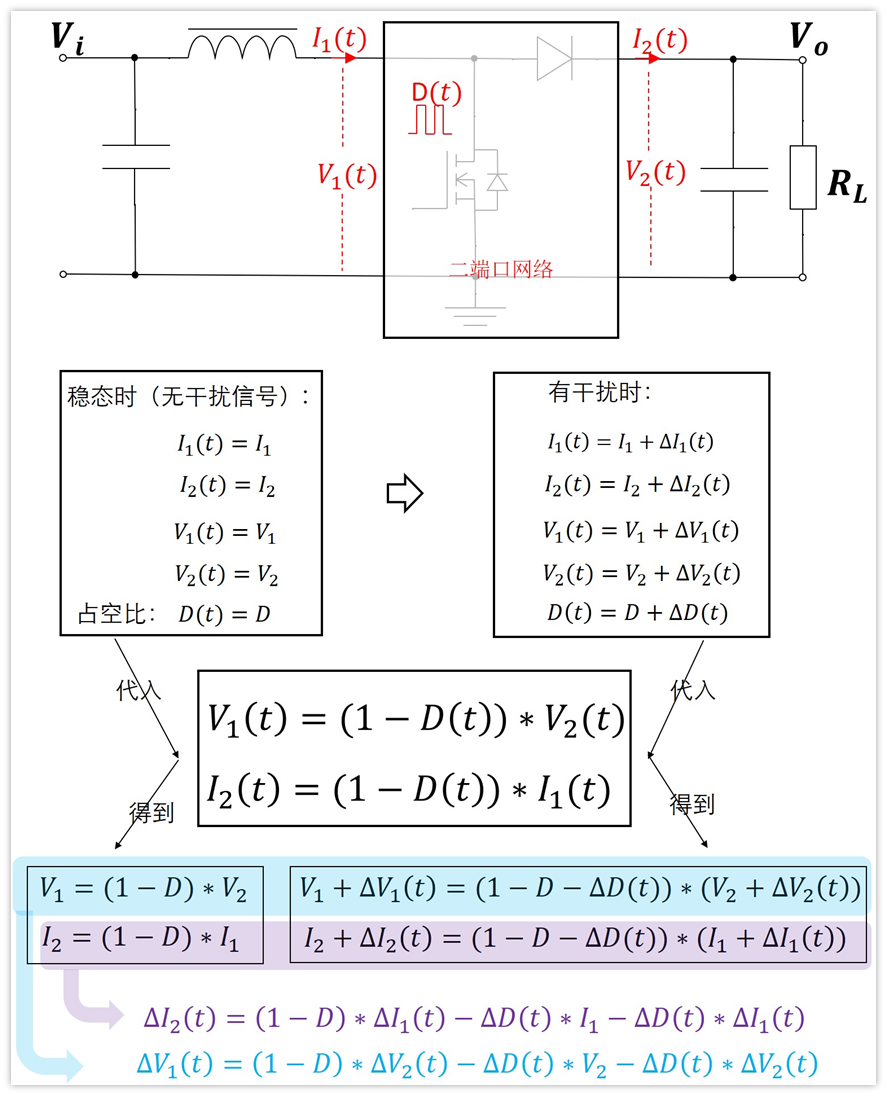
取的周期平均值我们用新符号表示,分别为:I1(t),I2(t),V1(t),V2(t),它们都是时间的函数。那么电路就变成了下面这样:
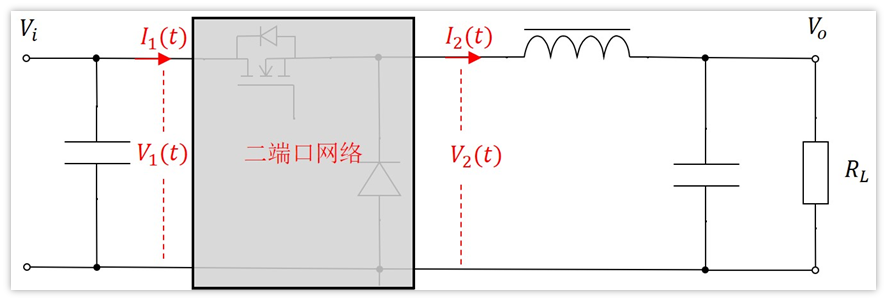
现在我们需要分析下我们引入二端口的4参数I1(t),I2(t),V1(t),V2(t),他们之间到底有啥恩怨情仇?
端口参数关系,推导出两个式子
假如没有任何干扰信号,那么I1(t),I2(t),V1(t),V2(t)周期平均值和全时间的平均值是一样的,每个周期都一样,每个周期的平均值自然和全部时间内的平均值一样,这应该没毛病。
好,我们假设没有干扰信号时,平均值分别是I1,I2,V1,V2,它们是个常量。此时开关信号的占空比也是恒定的,我们用D表示。
现在我们将干扰信号加进去,我们知道,系统只有满足小信号条件的时候,才能将之近似看成线性系统。
既然干扰信号是小信号,那么这个干扰信号会引起I1(t),I2(t),V1(t),V2(t)随时间小范围变化,它们分别以I1,I2,V1,V2为中心进行波动,同理,占空比也会围绕D为中心进行波动。
各变量的波动量不就是交流小信号吗?
我们分别用符号△I1(t),△I2(t),△V1(t),△V2(t),△D(t)来表示。
那么我们可以用下面的表达式进行表示:
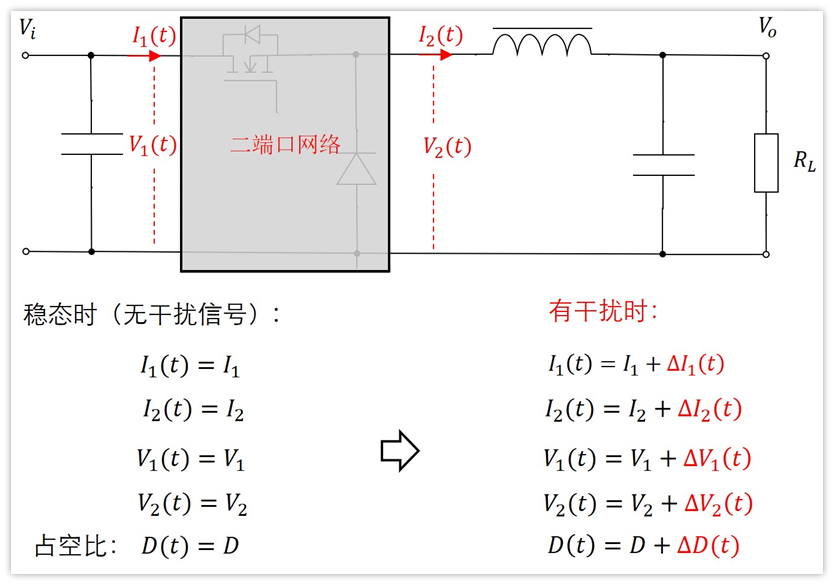
式子已经列出来了,现在我们需要求他们之间的关系。
先看看V2(t)的物理意义,前面说了,它是开关周期内的平均值。
显然,V2(t)=V1(t)*D(t),为什么呢?
因为在MOS不导通的时候,那么二极管导通,v2(t)为0,而在MOS导通的时候,v2(t)等于v1(t)。
所以,v2(t)在周期内的平均值V2(t)就等于导通时间的百分占比乘以V1(t),即:
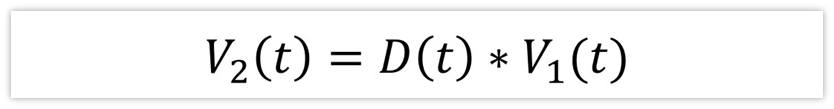
同样的,I1(t)= I2(t)*D(t),那又是为什么呢?
因为MOS在不导通的时候,i1(t)为0,而在MOS管导通的时候,i1(t)等于i2(t),所以,i1(t)在周期内的平均值I1(t) 就等于导通时间的百分占比乘以I2(t),即:
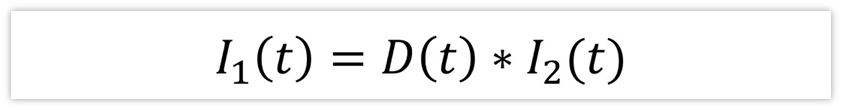
易知,上面两个式子,无论是在稳态(没有干扰),还是在有干扰的情况下,都是成立的。
小信号求解
我们把前面得到的几个式子代换一下,就可以得到小信号的表达式。
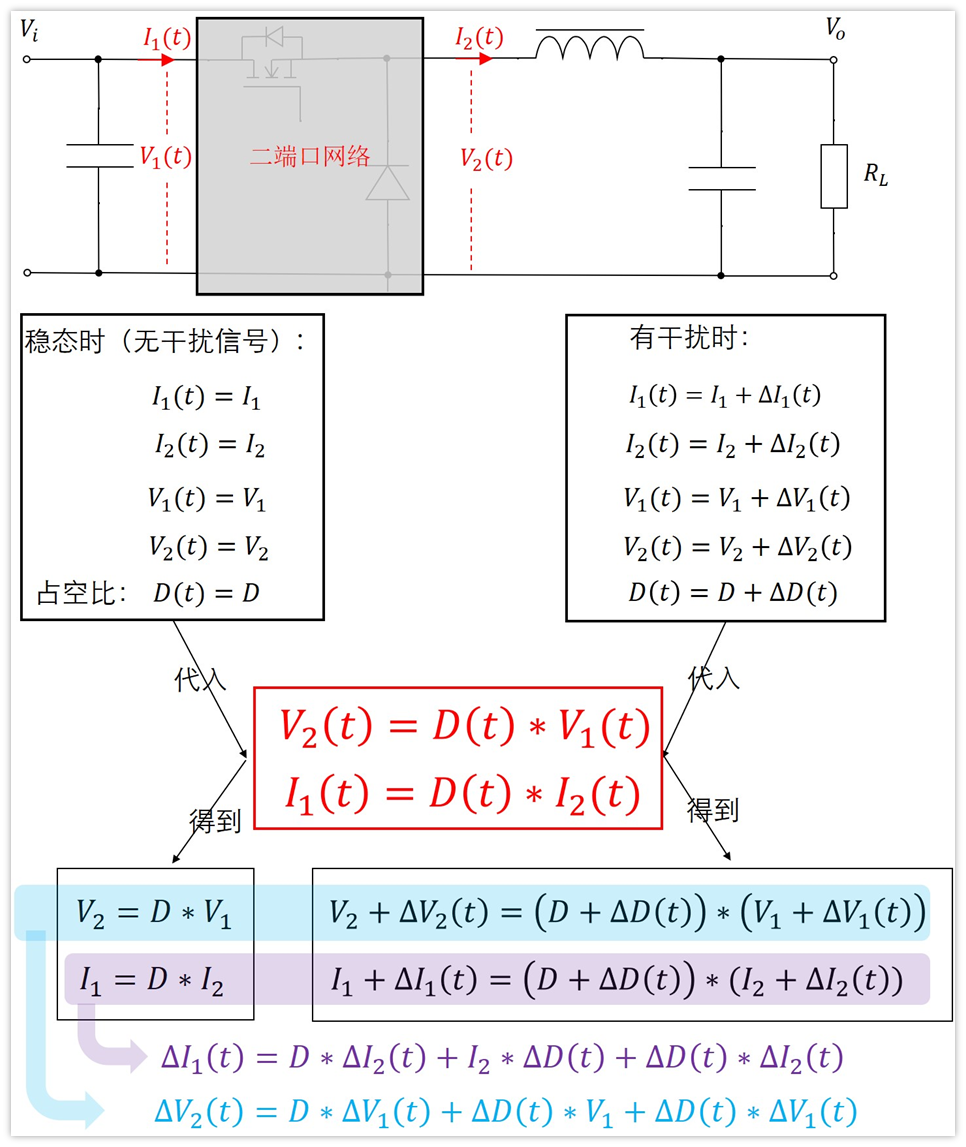
上面的式子可能看着有点复杂,其实简单代换就出来了,最终我们得到了下面这两个式子:

式子中忽略了高阶微小量,为什么可以忽略呢?
我是这么理解的,本来这些带△的量就是小信号,意思是围绕一个中心值小范围波动,所以带△符号的量相对于不带△符号的量是很小的。那么两个都带△符号的量相乘,乘积就更小了,所以干脆把它忽略掉了。
对于BUCK来说,只需要第一个式子就可以求出传递函数了,也就是下面这个
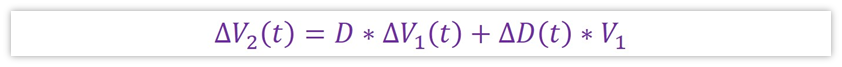
写的有点长,我们回顾下我们最终的目的,我们的目的是要求出Gvd,也就是△Vo/△D的值,上面式子中,我们已经能知道△V2与△D的关系,那△V2与△Vo是什么关系呢?
回到我们Buck的拓扑
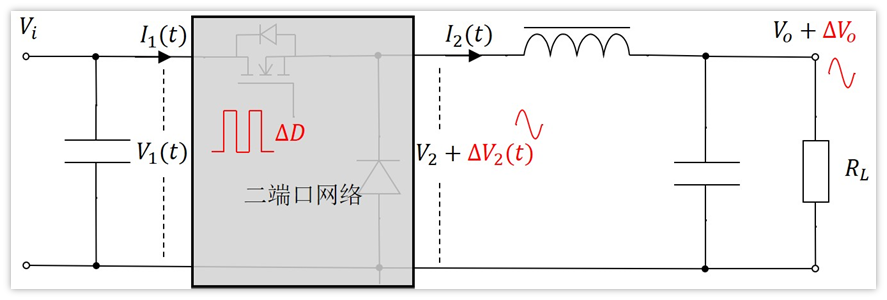
V1(t)不就是输入信号Vi吗?
理想情况下,Vi就是恒定的,占空比变化也不会导致Vi发生变化(不要考虑输入的开关纹波,我们现在分析的是理想拓扑,输入电源为理想电源,电压就是恒定的)。
既然Vi恒定,那么V1(t)就恒定不变,那么前面说的V1(t)的变化量△V1(t)=0。所以上面的那个式子可以再次化简下,如下:

另一方面,△V2指的是在占空比发生变化时,在电感前面引起的电压的变化量。
我们知道了△V2,那么△Vo不就是后面电感L,电容C,负载R对△V2的分压吗?那么就有了:
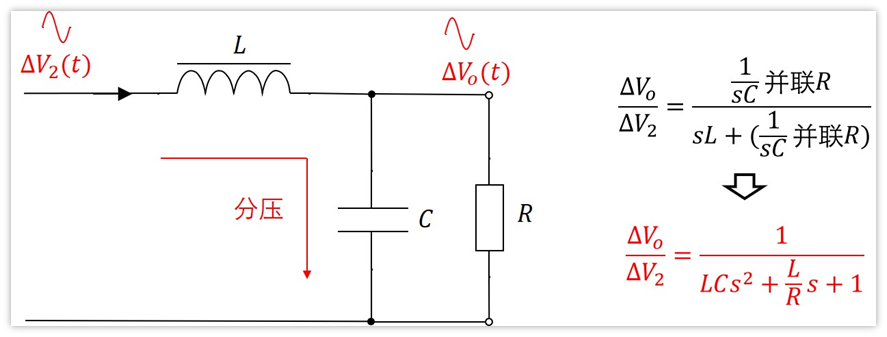
再结合前面得到的式子△V2=△D*Vi,我们就求得了最终的传递函数:
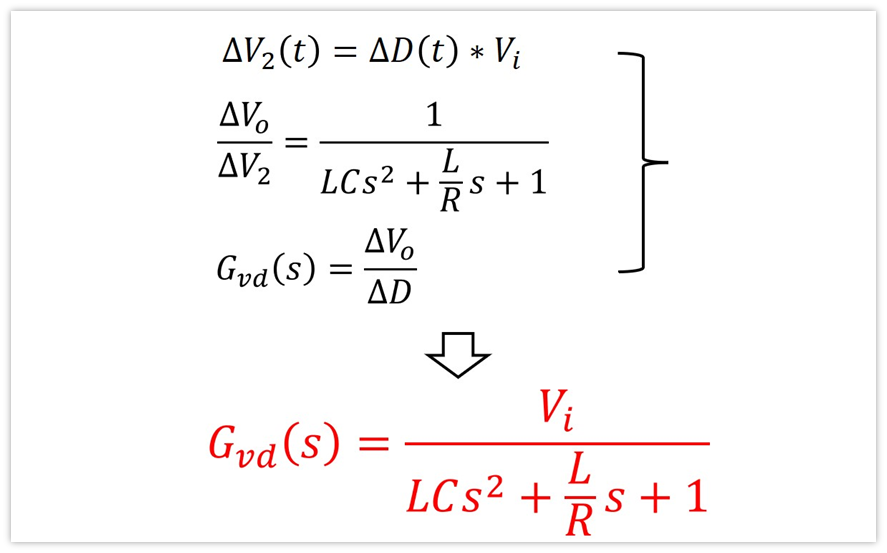
到此,我们就求出了buck的开关变换器的传递函数Gvd(s)。
写到这里,我估计会有兄弟说:搞了一堆,我肉眼都能看出在电感之前的信号表达式△V2=△D*Vi,再把它后面的电感L,C,R看成是低通滤波器,1分钟就能推出传递函数了。
确实如此,有点复杂,不过我上面的推导是普遍适用的法子,我拿BUCK来举例其实不好。如果拿boost就比较好,因为boost肉眼看不出来,但用上面的法子就可以推导出来。
那下面就再看看Boost
Boost的CCM模式传递函数推导过程
有了前面的铺垫,Boost我就写简单点,其实最关键的还是那个MOS和二极管,我们的过程依然是下面几步。
1、二端口等效
2、端口参数关系,推导出两个式子
3、代入电路,结合原理推导出传递函数
二端口等效
二端口等效如下:
端口参数关系,推导出两个式子
I1(t),I2(t),V1(t),V2(t)为周期平均值,假如没有任何干扰信号,它们和全时间的平均值是一样的,每个周期都一样,每个周期的平均值自然和全部时间内的平均值一样,这应该没毛病。
好,我们假设没有干扰信号时,平均值分别是I1,I2,V1,V2,它们是个常量。此时开关信号的占空比也是恒定的,我们用D表示。
现在我们将干扰信号加进去,我们知道,系统只有满足小信号条件的时候,才能将之近似看成线性系统。
既然干扰信号是小信号,那么这个干扰信号只会引起I1(t),I2(t),V1(t),V2(t)随时间小范围变化,它们分别以I1,I2,V1,V2为中心进行波动,同理,占空比也会围绕D为中心进行波动。
各变量的波动量不就是交流小信号吗?
我们分别用符号△I1(t),△I2(t),△V1(t),△V2(t),△D(t)来表示。
式子已经列出来了,现在我们需要求他们之间的关系。
先看看V1(t)的物理意义,它是周期内的平均值。
显然,V1(t)=V2(t)*(1-D(t)),为什么呢?
因为在MOS不导通的时候,二极管(看成理想二极管)导通,v1(t)为v2(t),而在MOS导通的时候,v1(t)接GND,为0,所以,v1(t)在周期内的平均值V1(t)就等于不导通时间的百分占比乘以V2(t),即:
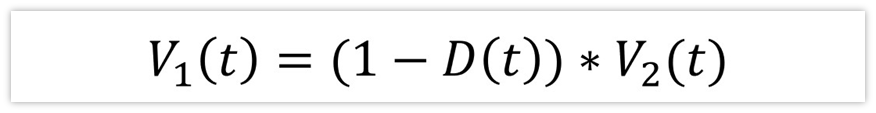
同样的,I2(t)= I1(t)* (1-D(t)),那又是为什么呢?
因为MOS在不导通的时候,i2(t)等于i1(t),而在MOS管导通的时候,i2(t)等于0,所以,i2(t)在周期内的平均值I2(t) 就等于不导通时间的百分占比乘以i1(t),即:
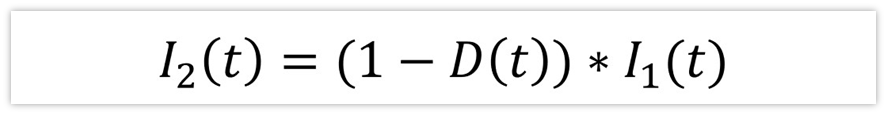
从推导过程看,上面两个式子,无论是在稳态(没有干扰),还是在有干扰的情况下,都是成立的。
小信号求解
我们把前面得到的几个式子代换一下,就可以得到小信号的表达式。
忽略高阶小项,得到下面两个小信号的式子:
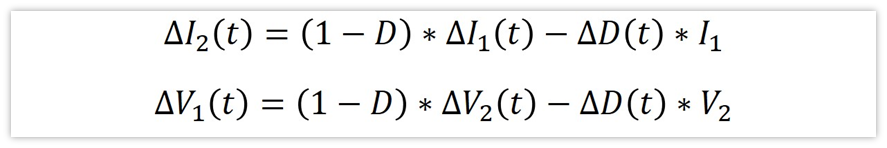
回想我们的目的,我们要得到传递函数,也就是需要知道△Vo与△D的比值关系。当然,我们会有一些量是已知的,比如输入Vi,占空比D,还有电感L,负载阻抗R,负载滤波电容C,这些都是已知量。
回到Boost的拓扑
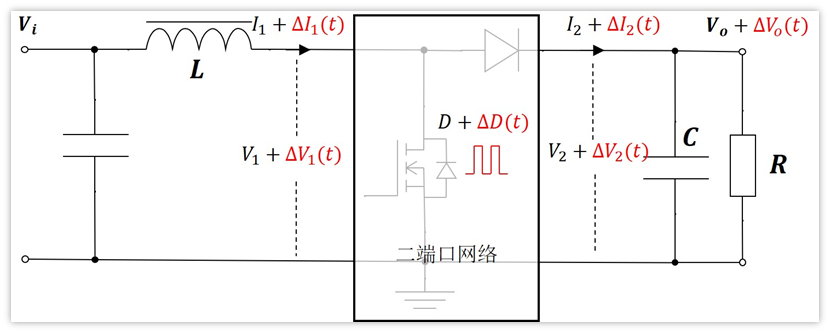
从上面我们能得到什么式子呢?
首先,在输入端,对于交流小信号来说,输入直流Vi相当于是短路,那么电感左边相当于接地,根据复阻抗的欧姆定律,那么电感两端压降就是:sL*△I1(t),也等于-△V1(t),负号表示方向。
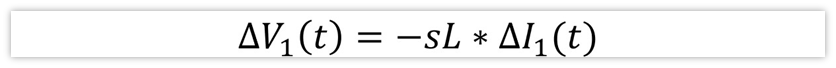
关于为什么“对于交流小信号来说,输入直流Vi相当于是短路”的,我之前也写过一篇文章,可以去瞅瞅。
其次,在输出端,对于交流小信号来说,电压△Vo=△V2,同时,根据复阻抗的欧姆定律,电压等于电流乘以阻抗,即:
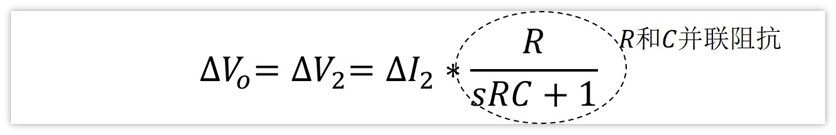
然后,V1为直流分量,因此有V1=Vi;
V2也为直流分量,因此有V2=Vo,I2=Vo/R
并且在小信号求解时,我们已经推出了两个公式:
V1=(1-D)*V2;
I2=(1-D)*I1
我们把上述所有公式汇总,消除中间量,就可以求出传递函数了,如下图:

以上就是boost求解传递函数的过程,看着是非常费劲,其实要是想通了就不难。
小结
很是费了一番功夫,最终求出了buck和boost的传递函数Gvd(s)。
我使用的方法其实就是《开关变换器的建模与控制+张卫平编著》里面的开关网络平均值法,不过我结合自己的喜好,改造了下,没有用变压器等效,尽量用通俗的语言,一步一步推出公式来。
当然,我这么玩不太严谨,如果想要深入了解的兄弟,建议去看下这本书,里面有很多建模方法,非常的专业。
但是不好的地方就是也比较难懂,我来来回回看了好久,终于有些许领悟,能做到扔掉书本,自己推出buck和boost的开关变换器的传递函数了,过程就是上面写的了。
以上内容其实在工作中是用不到的,各种拓扑的传递函数其实早已被前人给推导出来了,我们直接用就好。不过,人总有一些好奇心,会问个为什么,如果知道过程,那自然也是极好的。
想要《开关变换器的建模与控制+张卫平编著》这本书的pdf版本,可以在我的公众号“硬件工程师炼成之路”后台回复“炼成之路”,就可以下载了。
东西很多,在目录“书籍”里面,需要自己找一下。
推荐阅读:
1、我写的东西都在这里了
2、还在用CAM350吗?