来源 | 网络

智库 | 云脑智库(CloudBrain-TT)

云圈 | 进“云脑智库微信群”,请加微信:15881101905,备注您的研究方向

声明 | 本号聚焦相关知识分享，内容观点不代表本号立场，可追溯内容均注明来源，若存在版权等问题，请联系(15881101905，微信同号)删除，谢谢。

该文章原文是国外的一篇博文，对卡尔曼滤波的介绍使人通俗易懂，又有严谨的理论推导，是一篇不可多得的好文章，在此翻译过来和大家分享。原文链接：http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/。

以下为原文翻译。

我不得不说说卡尔曼滤波器，因为它的作用非常惊人。然而，似乎很少有软件工程师和科学家真正了解它，这让我感到难过，因为它是在存在不确定性的情况下组合信息的通用且强大的工具。它提取准确信息的能力令人惊奇。

什么是卡尔曼滤波器？

你可以在有不确定信息的动态系统的任何地方使用卡尔曼滤波器，从而对系统接下来要做什么做出有根据的猜测。即使有干扰出现并打乱了你猜测的运动，卡尔曼滤波器通常也能很好地找出实际发生的情况。它可以利用我们想象不到的现象之间的相关性！

卡尔曼滤波器非常适合连续变化的系统。它们的优点是内存占用少（除了前一个状态，不需要保留任何历史记录），而且速度非常快，非常适合实时问题和嵌入式系统。

在 Google 上找到的大多数地方，实现卡尔曼滤波器的数学运算看起来晦涩难懂。这是一种糟糕的情况，因为如果以正确的方式看待卡尔曼滤波器，它实际上非常简单且易于理解。因此，它是一个很棒的文章主题，我将尝试用许多清晰、漂亮的图片和颜色来照亮它。先决条件很简单：只需要对概率和矩阵有基本的了解。

我将从一个卡尔曼滤波器可以解决的问题的示例开始。

我们可以用卡尔曼滤波器做什么？

让我们举个玩具例子：你造了一个小机器人，它可以在树林里四处走动，机器人需要准确地知道自己的位置才能导航。

我们可以假设机器人有一个状态  ，它只表示位置和速度： 

请注意，状态只是有关系统底层配置的数字列表；它可以是任何东西。在我们的示例中，它是位置和速度，但它可能是关于油箱中的液体量、汽车发动机的温度、用户手指在触摸板上的位置或需要跟踪的任何数量的数据。

我们的机器人还有一个 GPS 传感器，精确到 10 米左右，这还不错，但它需要知道自己的位置比 10 米更精确。这些树林里有很多沟壑和悬崖，如果机器人错了几英尺以上，它可能会从悬崖上掉下来。所以只有 GPS 本身是不够的。

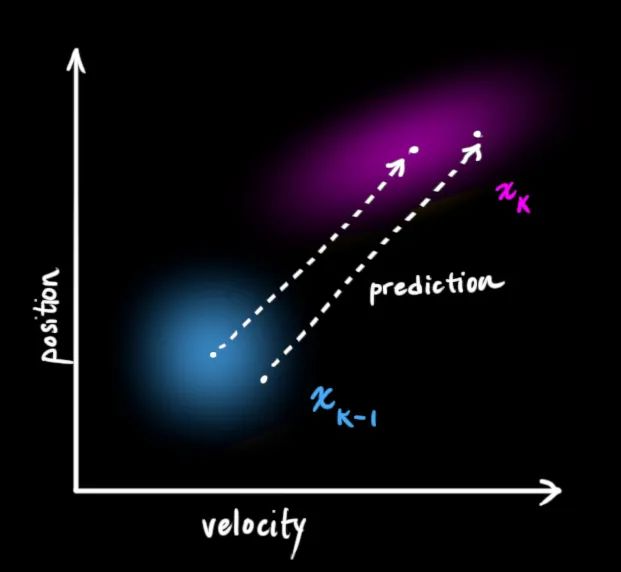
我们还知道机器人是如何移动的：发送命令到电机驱动轮子移动，机器人知道如果它朝一个方向前进且没有任何干扰，那么下一刻它可能会继续沿着该方向运动。

但机器人不知道它的运动的一切：它可能会受到风的冲击，车轮可能会打滑，或者在崎岖不平的地形上翻滚；所以轮子转动的量可能不能准确地代表机器人实际走了多远，预测也不会完美。

GPS 传感器告诉我们一些关于状态的信息，但只是间接的，并且带有一些不确定性或不准确性。我们的预测告诉我们一些关于机器人如何移动的信息，但也只是间接的，并且也存在一些不确定性或不准确性。

但是，如果我们使用所有可用的信息，我们能得到比任何一种估计本身都给我们更好的答案吗？当然答案是肯定的，这就是卡尔曼滤波器的用途。

卡尔曼滤波是如何看到你的问题的

下面我们继续以只有位置和速度这两个状态的简单例子做解释。 

我们并不知道实际的位置和速度，它们之间有很多种可能正确的组合，但其中一些的可能性要大于其它部分：

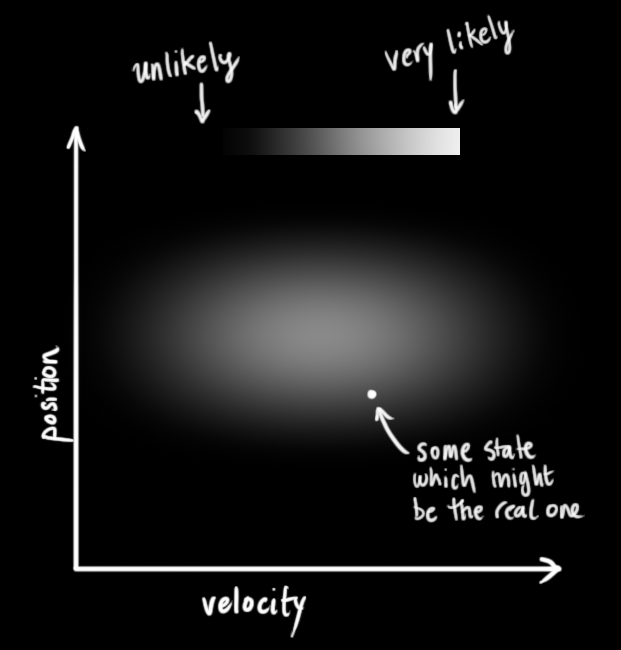
卡尔曼滤波假设两个变量（位置和速度，在这个例子中）都是随机的，并且服从高斯分布。每个变量都有一个均值  ，表示随机分布的中心（最可能的状态），以及方差  ，表示不确定性。

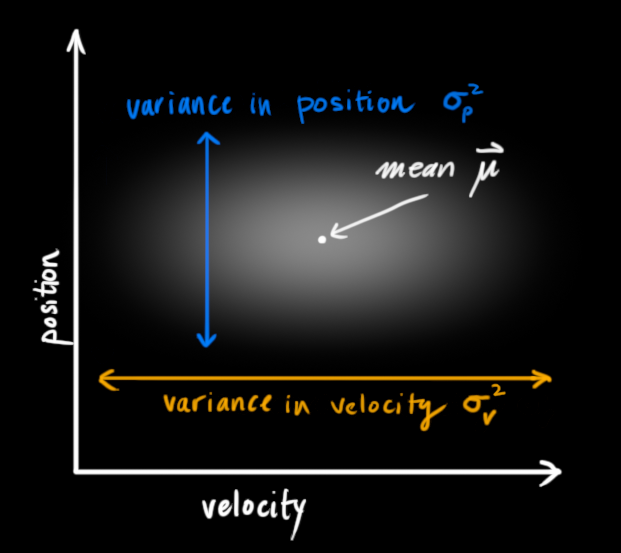
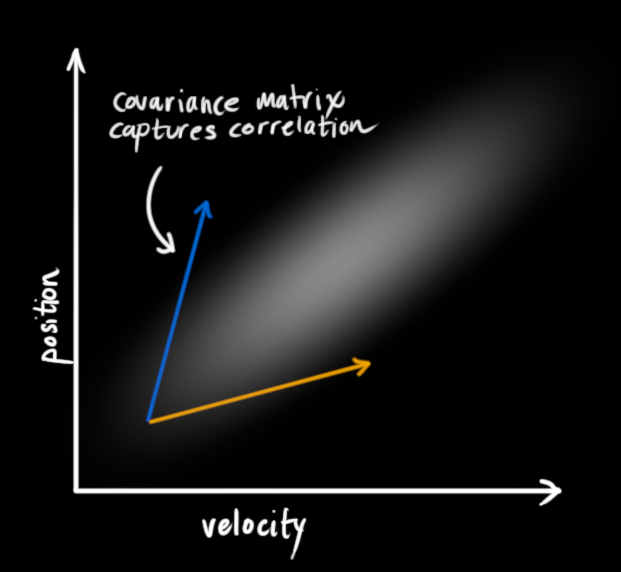
在上图中，位置和速度是不相关的，这意味着由其中一个变量的状态无法推测出另一个变量可能的值。下面的例子更有趣：位置和速度是相关的，观测特定位置的可能性取决于当前的速度：

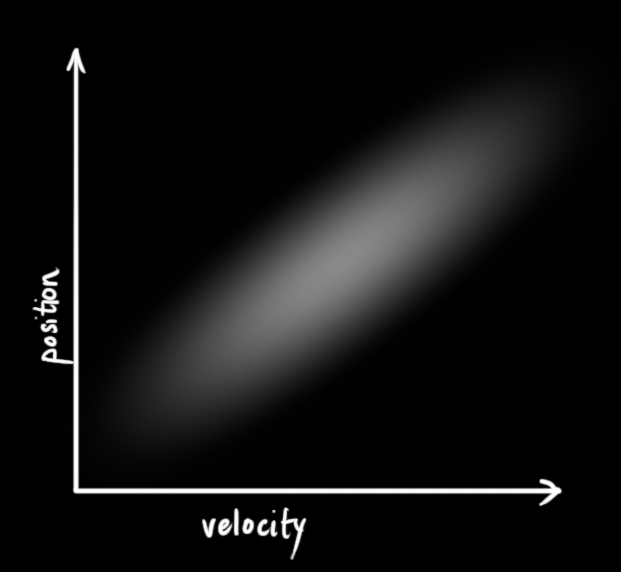
这种情况是有可能发生的，例如，我们根据旧的位置来估计新位置。如果速度很快，我们可能已经移动很远了。如果速度很慢，则距离不会很远。跟踪这种关系是非常重要的，因为它带给我们更多的信息：其中一个测量值告诉了我们其它变量可能的值，这就是卡尔曼滤波的目的，尽可能地在包含不确定性的测量数据中提取更多信息！

这种相关性用协方差矩阵来表示。矩阵中的每个元素  表示第  个状态变量和第  个状态变量之间的相关度。又因为第  个状态变量和第  个状态变量之间的相关度等于第  个状态变量和第  个状态变量之间的相关度，故协方差矩阵是一个对称矩阵。

协方差矩阵通常用  来表示，其中的元素则用  表示。

使用矩阵来描述问题

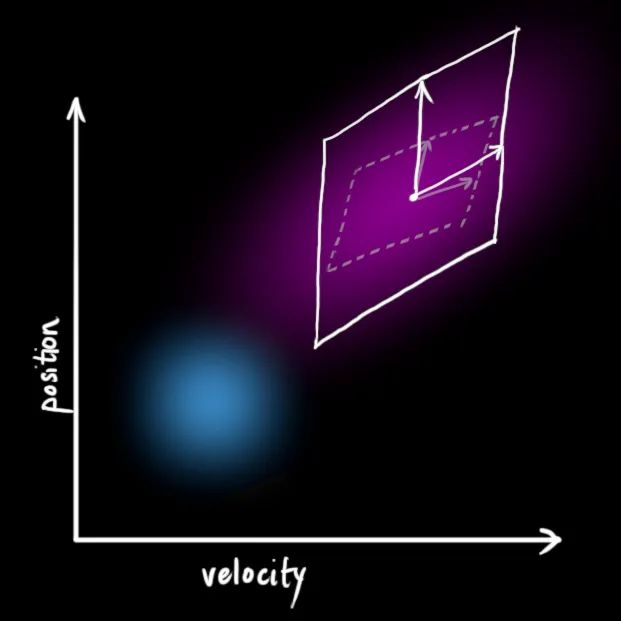
我们基于高斯分布来建立状态变量，所以在  时刻需要两个信息：最佳估计  （即均值，其它地方常用  表示），以及协方差矩阵  。 

当然，在这里我们只用到了位置和速度，实际上这个状态可以包含多个变量，代表任何你想表示的信息。接下来，我们需要根据当前状态（k-1 时刻）来预测下一状态（k 时刻）。记住，我们并不知道对下一状态的所有预测中哪个是“真实”的，但我们的预测函数并不在乎。它对所有的可能性进行预测，并给出新的高斯分布。

我们可以用矩阵  来表示这个预测过程：

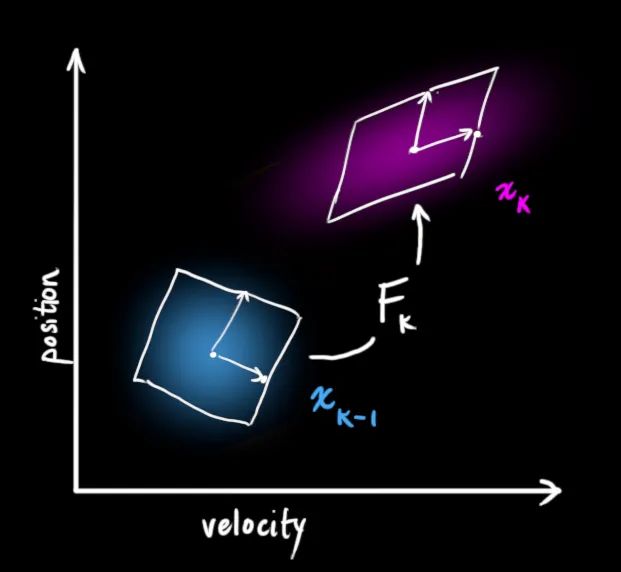
它将我们原始估计中的每个点都移动到了一个新的预测位置，如果原始估计是正确的话，这个新的预测位置就是系统下一步会移动到的位置。那我们又如何用矩阵来预测下一个时刻的位置和速度呢？下面用一个基本的运动学公式来表示： 

 换句话说： 

现在，我们有了一个预测矩阵来表示是下一个时刻的状态，但是，我们仍然不知道怎么更新协方差矩阵。此时，我们需要引入另一个公式，如果我们将分布中的每个点都乘以矩阵  ，那么它的协方差矩  会怎样变化呢？很简单，下面给出公式： 

结合上面的方程，可得 

外部影响

我们并没有捕捉到一切信息，可能存在外部因素会对系统进行控制，带来一些与系统自身状态没有相关性的改变。

以火车的运动状态模型为例，火车司机可能会操纵油门，让火车加速。相同地，在我们机器人这个例子中，导航软件可能会发出一个指令让轮子转向或者停止。如果知道这些额外的信息，我们可以用一个向量  来表示，将它加到我们的预测方程中做修正。

假设由于油门的设置或控制命令，我们知道了期望的加速度  ，根据基本的运动学方程可以得到： 

以矩阵的形式表示就是： 

  称为控制矩阵，  称为控制向量（对于没有外部控制的简单系统来说，这部分可以忽略）。让我们再思考一下，如果我们的预测并不是100%准确的，该怎么办呢？

外部不确定性

如果这些状态量是基于系统自身的属性或者已知的外部控制作用来变化的，则不会出现什么问题。

但是，如果存在未知的干扰呢？例如，假设我们跟踪一个四旋翼飞行器，它可能会受到风的干扰，如果我们跟踪一个轮式机器人，轮子可能会打滑，或者路面上的小坡会让它减速。这样的话我们就不能继续对这些状态进行跟踪，如果没有把这些外部干扰考虑在内，我们的预测就会出现偏差。

在每次预测之后，我们可以添加一些新的不确定性来建立这种与“外界”（即我们没有跟踪的干扰）之间的不确定性模型：

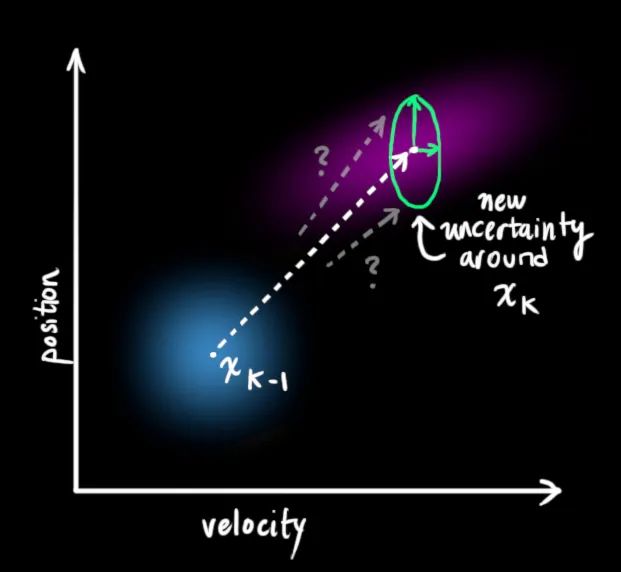
我们最初估计的每个状态变量更新到新的状态后， 仍然服从高斯分布，所以我们可以说  中的每个状态变量都移动到了一个新的服从高斯分布的区域，协方差为  。另一种说法是，我们将这些没有被跟踪的影响视为具有协方差  的噪声来处理。

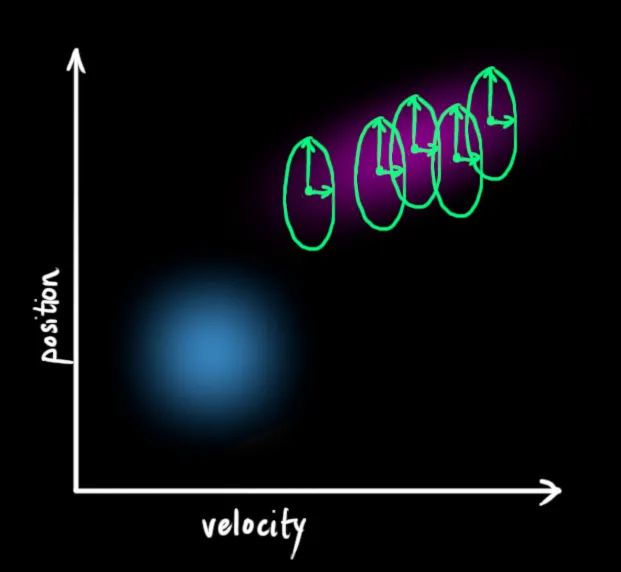
这产生了具有不同协方差（但是具有相同的均值）的新的高斯分布。

我们通过简单地添加  得到扩展的协方差，下面给出预测步骤的完整表达式： 

由上式可知，新的最优估计是根据上一最优估计预测得到的，并加上已知外部控制量的修正。而新的不确定性由上一不确定性预测得到，并加上外部环境的干扰。

现在我们对系统可能的动向有了一个模糊的估计，用  和  来表示。如果再结合传感器的数据会怎样？

用测量值来修正估计值

我们可能会有多个传感器来测量系统当前的状态，哪个传感器具体测量的是哪个状态变量并不重要，也许一个是测量位置，一个是测量速度，每个传感器间接地告诉了我们一些状态信息。

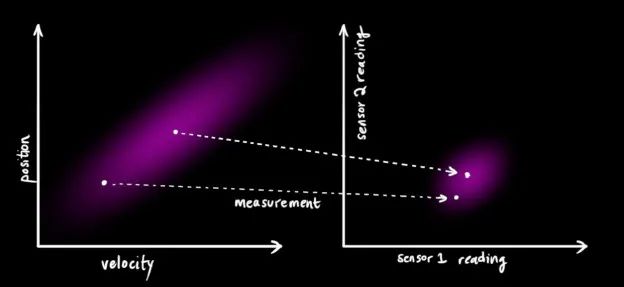
注意，传感器读取的数据的单位和尺度有可能与我们要跟踪的状态的单位和尺度不一样，我们用矩阵  来表示传感器的数据。

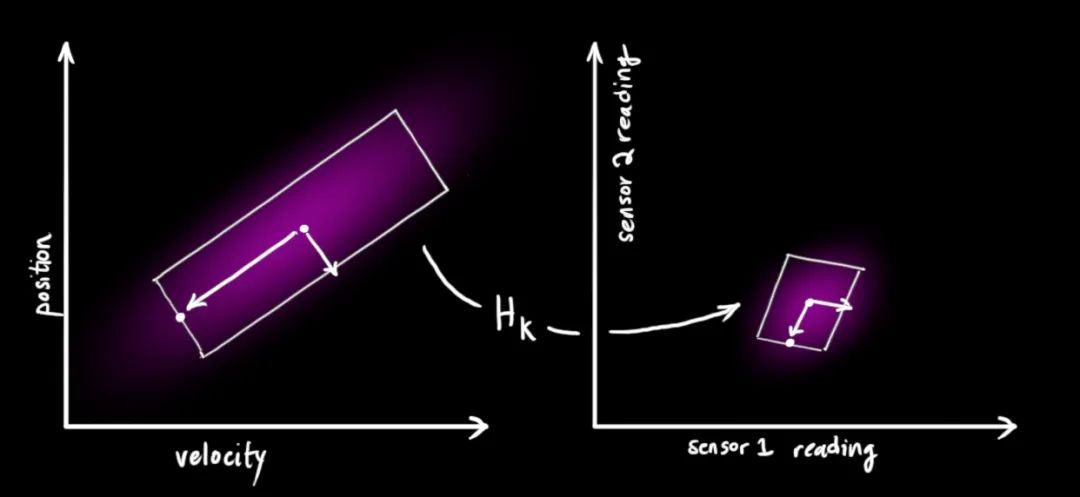
我们可以计算出传感器读数的分布，用之前的表示方法如下式所示： 

卡尔曼滤波的一大优点就是能处理传感器噪声，换句话说，我们的传感器或多或少都有点不可靠，并且原始估计中的每个状态可以和一定范围内的传感器读数对应起来。

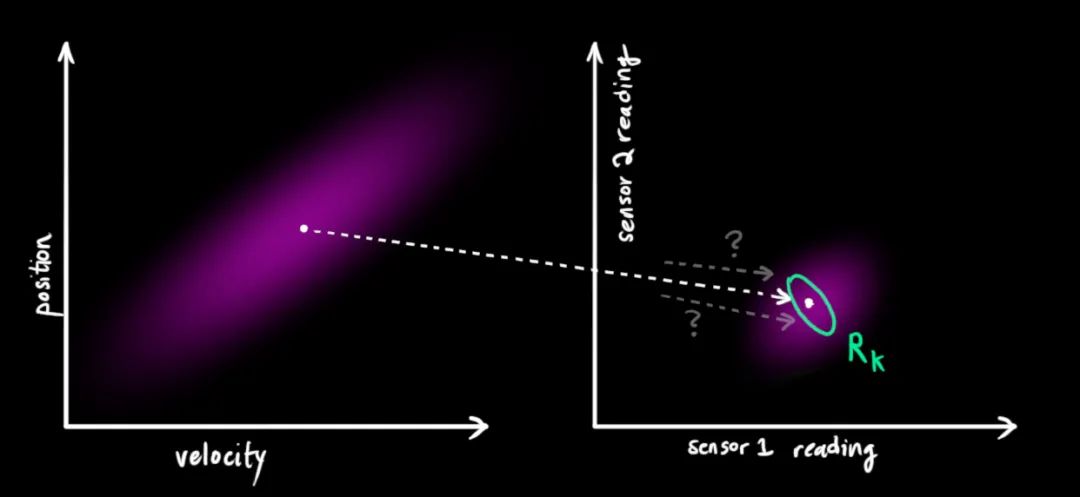
从测量到的传感器数据中，我们大致能猜到系统当前处于什么状态。但是由于存在不确定性，某些状态可能比我们得到的读数更接近真实状态。

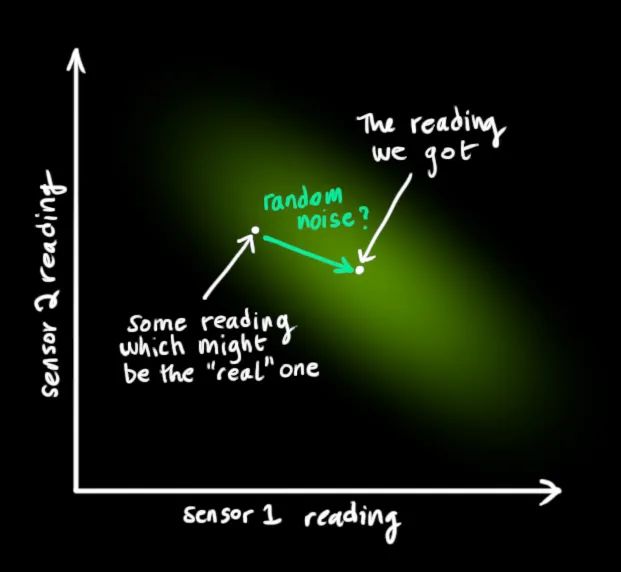
我们将这种不确定性（如：传感器噪声）用协方差  表示，该分布的均值就是我们读取到的传感器数据，称之为  。

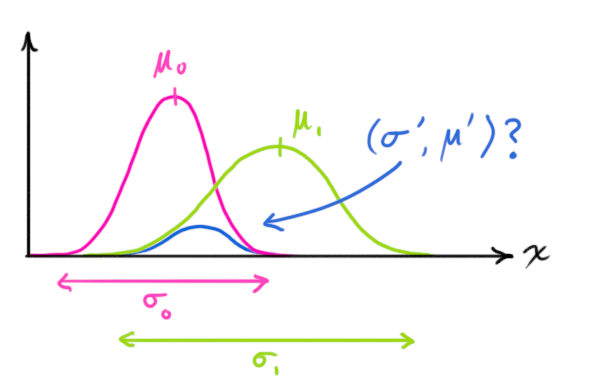
现在我们有了两个高斯分布，一个是在预测值附近，一个是在传感器读数附近。

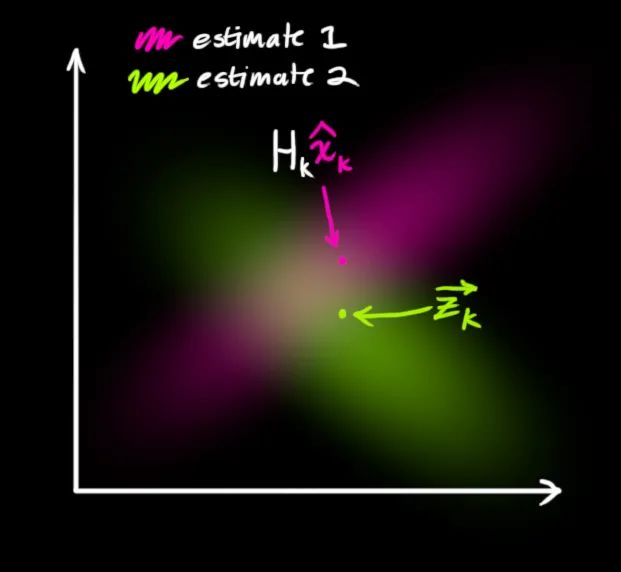
我们必须在预测值（粉红色）和传感器测量值（绿色）之间找到最优解。

那么，我们最有可能的状态是什么？对于任何可能的读数  ，有两种情况：（1）传感器的测量值；（2）由前一状态得到的预测值。如果我们想知道这两种情况都可能发生的概率，将这两个高斯分布相乘就可以了。

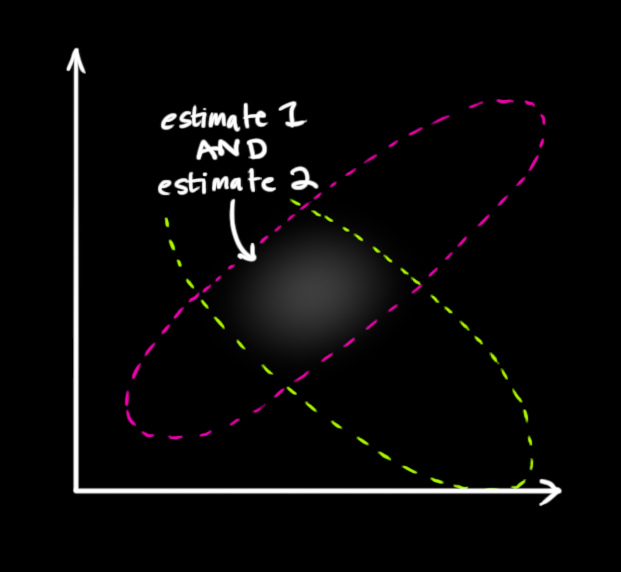
剩下的就是重叠部分了，这个重叠部分的均值就是两个估计最可能的值，也就是给定的所有信息中的最优估计。

瞧！这个重叠的区域看起来像另一个高斯分布。

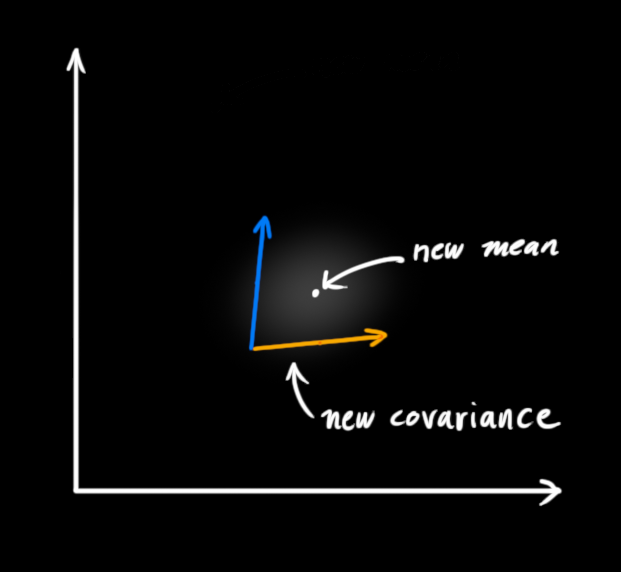
如你所见，把两个具有不同均值和方差的高斯分布相乘，你会得到一个新的具有独立均值和方差的高斯分布！下面用公式讲解。

融合高斯分布

先以一维高斯分布来分析比较简单点，具有方差  和  的高斯曲线可以用下式表示： 

如果把两个服从高斯分布的函数相乘会得到什么呢？

将高斯曲线表达式代入到上式中（注意重新归一化，使总概率为 1）可以得到： 

将式（11）中的两个式子相同的部分用  表示：

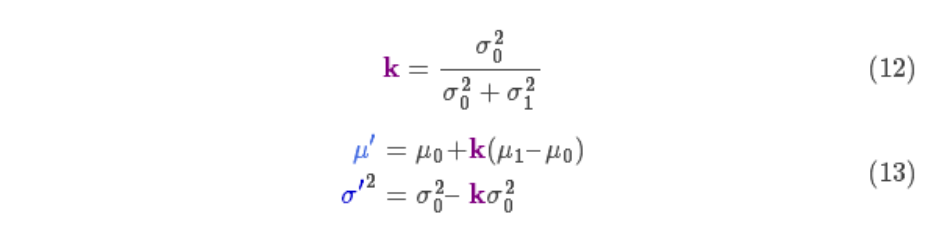
将上式写成矩阵形式，如果  表示高斯分布的协方差，  表示每个维度的均值，则：

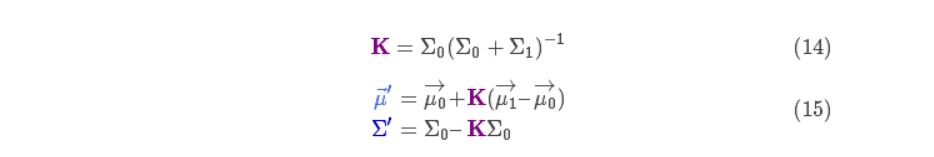
矩阵  称为卡尔曼增益，下面将会用到。放松！我们很快要完成了！

将所有公式整合起来

我们有两个高斯分布，预测部分  ，和测量部分  ，我们将它们放到式（15）中算出它们之间的重叠部分： 

由式（14）可得卡尔曼增益为： 

 将上两式的两边同时左乘矩阵的逆（注意  里面包含了  ）将其约掉，再将式中第二个等式两边同时右乘矩阵  的逆得到以下等式：

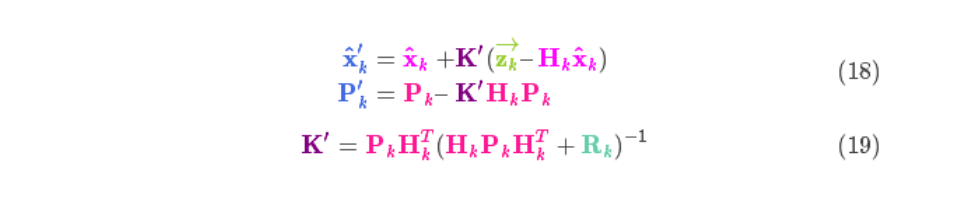
上式给出了完整的更新步骤方程。  就是新的最有估计，我们可以将它和  放到下一个预测和更新方程中不断迭代。

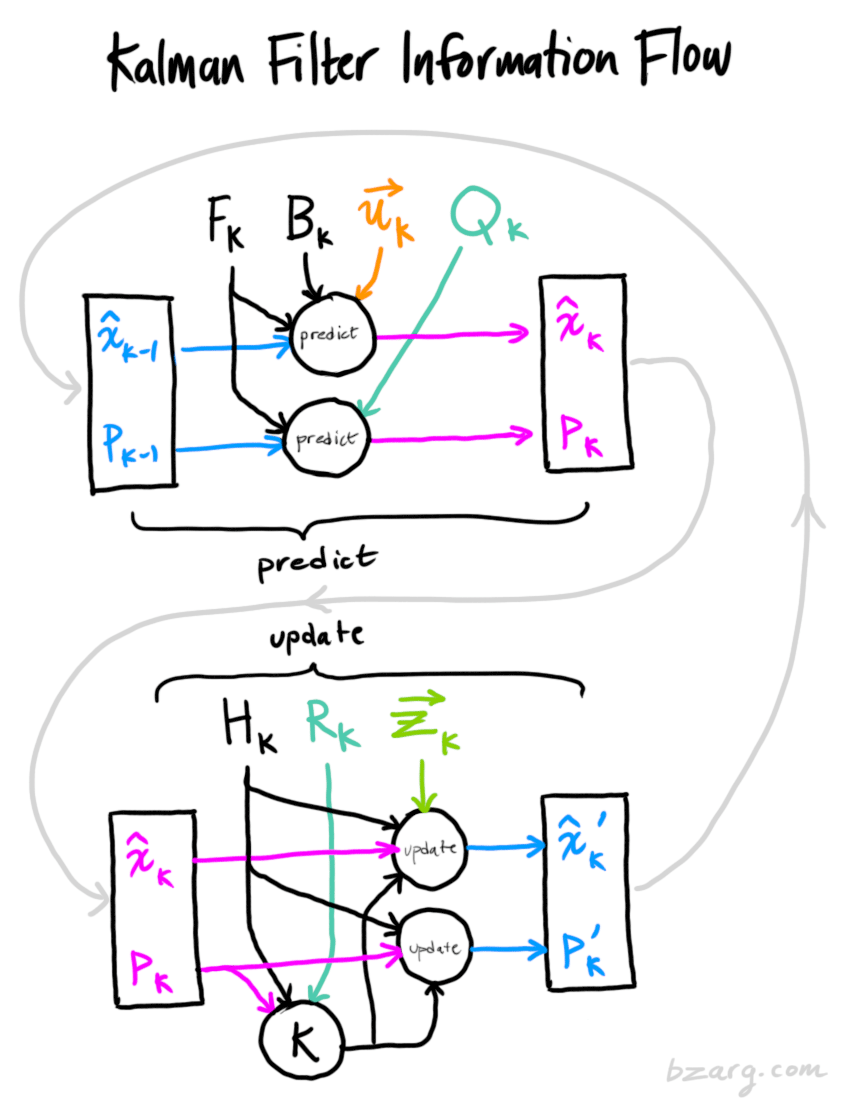
该文章翻译参考

https://blog.csdn.net/u010720661/article/details/63253509。

－ The End －

版权声明：欢迎转发本号原创内容，转载和摘编需经本号授权并标注原作者和信息来源为云脑智库。本公众号目前所载内容为本公众号原创、网络转载或根据非密公开性信息资料编辑整理，相关内容仅供参考及学习交流使用。由于部分文字、图片等来源于互联网，无法核实真实出处，如涉及相关争议，请跟我们联系删除。我们致力于保护作者知识产权或作品版权，本公众号所载内容的知识产权或作品版权归原作者所有。本公众号拥有对此声明的最终解释权。

投稿/招聘/推广/合作/入群/赞助 请加微信：15881101905，备注关键词

“阅读是一种习惯，分享是一种美德，我们是一群专业、有态度的知识传播者.”