对车进行受力分析
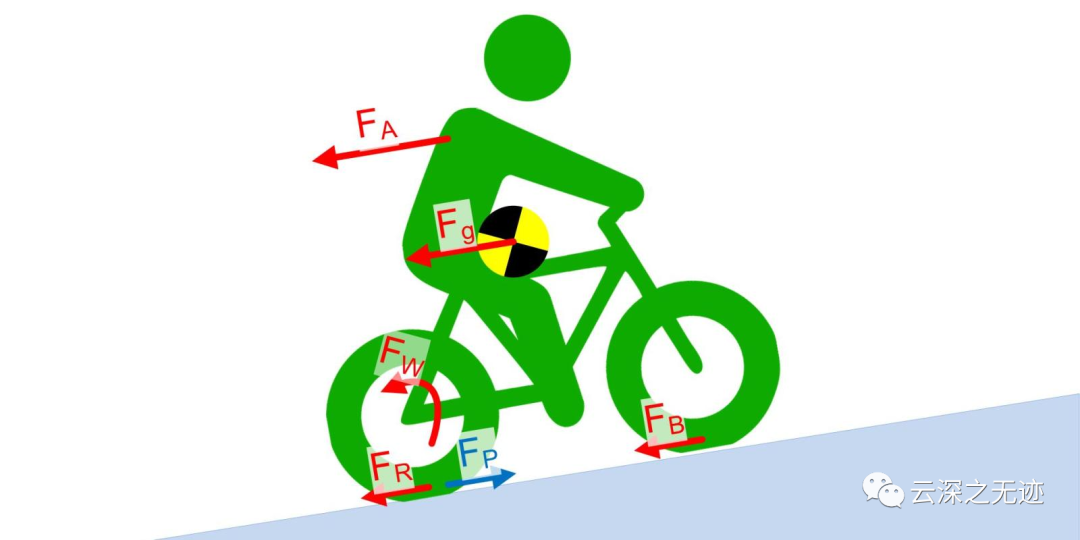
将基础物理学应用于自行车运动,方程F = ma(力 = 质量x加速度)可以表示为
F P – F R = ma
其中F P是推进力,F R是所有阻力的总和。
假设已经达到恒定速度,加速度为零,上述方程简单地变为F P = F R。将其乘以速度v,将推进力转换为推进功率P P。
P P = v F R
P P可以由骑车人产生的输入功率P in和传输系统的效率η代替。这给出了一个将自行车的稳态速度与骑手产生的功率联系起来的一般方程:
P in η = v F R
运动的总阻力实际上由几个单独的阻力组成:
F g,重力阻力(在斜坡上骑行时)
F A , 向前运动的空气阻力
F R , 滚动阻力
F RB , 车轮轴承阻力
F B , 耐冲击性
F W , 车轮转动的空气阻力
这些阻力有时以不同的方式表示,但基本力量保持不变。

重力作用在自行车和骑手的总质量上,产生向下的力,重量。如果地面不水平,则该力的一部分将作用以抵抗向前运动。如果将斜率指定为角度,则重力mg将乘以角度的余弦值。通常,坡度将指定为梯度G,因此重力阻力由下式给出
F g = mg sin( arctan( G ) )
其中m是自行车和骑手的总质量,g是重力加速度 (9.81 m/s),G是坡度的坡度。最陡峭的道路的坡度约为 30%,但这种情况非常罕见。12% 的梯度通常被认为是非常陡峭的。
F g在任何速度下都是相同的,即使在静止时,它只是将您拉下山坡的力。
空气阻力或空气动力阻力由标准方程给出:
F A = ½ C d A ρ v A 2
其中C d是阻力系数,A是正面面积,ρ是空气密度,v A是自行车行驶方向上的空气速度。有时使用f 来明确表示阻力系数是基于正面面积的,这是因为通常使用不同的表面积度量来指定翼型截面。
由于自行车形状或骑手位置的变化会同时改变阻力系数和正面面积,因此通常将C d A视为单个参数(阻力面积)更方便。这可以通过测试找到。例如,在风洞中,力F A和风速v 被测量。还测量了气压、温度和湿度,用于计算空气密度 ρ。然后通过重新排列标准空气阻力方程来计算阻力面积:
C d A = 2 F A / ρ v A 2
一般不需要精确测量额叶面积并独立确定C d。阻力面积足以计算任何速度和任何环境下的阻力。
重要的是要注意C d 实际上随速度而变化,尽管在小范围的速度上将其视为常数通常是可以接受的。随着空气速度的增加,气流以显着方式变化,例如变得湍流和层流分离。这可能导致C d发生相当突然的变化。对于给定的形状,影响阻力区域的关键参数是雷诺数,它取决于速度和物体的大小。自行车和骑车人的主要部件大致呈圆柱形,直径从 1 毫米(辐条)到约 300 毫米(骑车人的身体)不等,在典型的骑行速度下,这导致雷诺数在 10 3到 10的大致范围内5 . 在此范围内,气缸的阻力系数近似恒定。然而,在更高的速度下,系数会发生显着变化。此外,对于翼型截面,阻力系数在此范围内变化很大。因此,对于更流线型的自行车,将阻力区域评估为速度的函数可能是有价值的。
风以两种方式使事情复杂化。首先,逆风意味着空气速度v A与自行车速度v G不同。其次,侧风会改变自行车的阻力区域,因为空气以不同的方向流过自行车和骑手。相对于自行车的路径,风可以具有任何方向。考虑这些问题的第一步是将风速分成两个分量。逆风分量与自行车的路径相切,速度为v WTan,侧风分量垂直于自行车的路径,速度为v WNor。然后可以根据自行车的速度和逆风分量计算空气速度:
v A = v G + v WTan
偏航角是自行车路径与自行车上方气流方向之间的角度。计算如下:
偏航角= arctan( v WNor / v A )
在风洞中测量阻力时,应在不同的偏航角下进行测量。然后可以在测量的角度之间进行插值,以确定任何偏航角的C d A。
有时,会进行进一步的简化,其中C d A与因子 ½ 和空气密度相结合,得到单个气动阻力因子k A,由下式给出
k A = ½ C d A ρ
这可能很方便,但也可能会错误地产生空气密度相对恒定的印象。不是这种情况。在极端条件下,空气密度可能高达 1.5 kg/m 3(海平面以下,干燥空气温度为 -30 C)或低至 0.9 kg/m 3(海拔 1,000 m,温度为 50 C 和 100湿度百分比)。在世界上最高的道路上,密度甚至可以低至 0.7 kg/m 3。即使在正常条件下,密度也可以在大约 1.1 和 1.3 kg/m 3之间变化。
对于风洞测试,自行车应安装在滚轮上,使其车轮以地面速度旋转。这是因为车轮的运动改变了自行车和骑手上的空气流动。然而,在风洞中测量的力只是空气向后推自行车和骑手的力。没有测量空气对车轮旋转的阻力,主要是由辐条穿过空气引起的。这种阻力有自己的阻力区域,可以通过在空中旋转车轮来测量。车轮旋转的空气阻力由下式给出:
F W = ½ C d A ρ v G 2
请注意,这里可能应该使用地速。很明显,如果顺风正好与自行车的速度相匹配,因此空气速度为零,那么车轮的旋转仍然存在阻力。这表明在某些来源中使用空气速度是不正确的。然而,空气速度很可能会产生一些影响,而在静止空气中旋转车轮则无法检测到这种影响。这个问题在文献中还没有得到充分的探讨。
还应该注意的是,如果使用滑行或类似测试来确定阻力区域,那么这将产生一个组合阻力区域,用于抵抗自行车的向前运动和车轮的旋转。在这种情况下,很难完全处理偏航角的影响。
当车轮在地面上滚动时,车轮和地面都会轻微变形。这种变形中的一些是弹性的,因此能量被回收。非弹性变形产生热量并耗散功率。钢轨上的实心钢轮具有非常小的非弹性变形,因此滚动阻力非常低。充气轮胎内的空气也具有良好的能量回收性。然而,一些能量仍因外胎内的摩擦而损失。在柔软的地面上骑行时,地面本身也会消耗大量能量。
当车轮通过粗糙表面的小颠簸时,小的惯性载荷也可能包含在滚动阻力中,尽管严格来说这是颠簸阻力,将在下一节中讨论。
不存在可靠的滚动阻力分析模型。相反,测量给定轮胎、路面和充气压力的滚动阻力。滚动阻力通常被建模为滚动阻力的单一无量纲系数C R ,它是轮胎上的法向力与切向力的比值。法向力是自行车和骑手压在路面上的重量之和。在完全水平的道路上,这是简单的mg。切向力是滚动阻力。在坡度为G的山坡上,滚动阻力由下式给出:
F R = C R mg cos( arctan( G ) )
由于路面的不平整而不断遇到的小颠簸通常包含在滚动阻力中。大的光滑颠簸可能不会引起任何阻力。轮子可以平稳地向上滚动,将动能转化为势能。当车轮从另一侧向下滚动时,势能将转换回动能,几乎完全恢复能量。更大和更陡峭的颠簸可能会导致显着的阻力,这需要与滚动阻力分开考虑。例如,道路上的路缘石和坑洼,或越野的岩石和树根。
当车轮遇到方边凸块时,受力的角度取决于凸块的大小和车轮的大小。如果方形边缘凸起高于车轮半径,则车轮可能完全停止。这经常发生在旱冰鞋和滑板的小轮子上。如果悬架允许车轮在向上移动之前相对于车辆向后移动,那么即使在这种极端情况下,车轮也有可能在颠簸上翻滚。
必须在颠簸上举起的质量越低,颠簸阻力就越低。出于这个原因,充气轮胎在最大限度地减少颠簸阻力方面表现出色,因为只有一小部分重达几克的外胎被抬起来越过大多数颠簸。对于充气轮胎无法吸收的过大颠簸,悬挂意味着只需将车轮和悬挂臂举过颠簸,而不是整车。
没有分析或实验方法来确定一般的碰撞阻力。一个重大的挑战是阻力在很大程度上取决于骑手的反应。
车轮轴承阻力通常包含在滚动阻力中,尽管它是一个单独的阻力,表现不同。已经表明,轴承产生的扭矩随法向力和旋转速度线性变化 Mai、Poland 和 Jenkins (1991)。然而,由于轴承阻力相对较小,将其视为滚动阻力的一个组成部分似乎产生的误差可以忽略不计。在迄今为止最准确的测试中,没有包括与速度相关的轴承阻力分量,而轴承阻力包含在滚动阻力中。
这种方法首先被证明可以将公路自行车手的力量预测大约 3%(Martin 等人,1998 年)。这些测试使用风洞测试来确定一系列偏航角的C d A ,并使用独立测试来确定车轮旋转的空气阻力,但参考值用于滚动和车轮轴承阻力。Fitton & Symons (2018)通过考虑动能变化并准确模拟转弯时滚动阻力的变化,实现了相当高的精度。
出于多种原因,可能会将阻力组合在一起。有时这样做只是为了呈现一个更简单的模型。例如,轴承阻力非常小,通常包含在滚动阻力中。对阻力进行分组的一个很好的理由是在执行滑行测试时。降低成本测试涉及记录自行车从某个已知速度减速所需的时间,而无需踩踏板、制动或转弯。减速是由阻力引起的,允许它们被确定。通过考虑它们如何随速度变化,可以将减速归因于各个阻力因素。测量测试轨道坡度并首先去除计算出的重力阻力。不随速度变化的恒定力则归因于滚动阻力,虽然轴承阻力和可能的碰撞阻力也将包括在内。剩余的力将随速度的平方变化,归因于空气阻力。然而,这与在风洞中测量的空气阻力不同,因为它包括向前运动的空气阻力和车轮旋转的空气阻力。表达这些力的更一般的方式是零阶力和二阶力,指的是它们变化的速度的力量。理论上,也可以识别一阶力,其中可能包括轴承摩擦的速度相关分量。在实践中,滑行测试不够准确,无法检测到这种影响。因此,滑行测试确定了两个阻力参数。剩余的力将随速度的平方变化,归因于空气阻力。然而,这与在风洞中测量的空气阻力不同,因为它包括向前运动的空气阻力和车轮旋转的空气阻力。表达这些力的更一般的方式是零阶力和二阶力,指的是它们变化的速度的力量。理论上,也可以识别一阶力,其中可能包括轴承摩擦的速度相关分量。在实践中,滑行测试不够准确,无法检测到这种影响。因此,滑行测试确定了两个阻力参数。剩余的力将随速度的平方变化,归因于空气阻力。然而,这与在风洞中测量的空气阻力不同,因为它包括向前运动的空气阻力和车轮旋转的空气阻力。表达这些力的更一般的方式是零阶力和二阶力,指的是它们变化的速度的力量。理论上,也可以识别一阶力,其中可能包括轴承摩擦的速度相关分量。在实践中,滑行测试不够准确,无法检测到这种影响。因此,滑行测试确定了两个阻力参数。这与在风洞中测量的空气阻力不同,因为它包括向前运动的空气阻力和车轮旋转的空气阻力。表达这些力的更一般的方式是零阶力和二阶力,指的是它们变化的速度的力量。理论上,也可以识别一阶力,其中可能包括轴承摩擦的速度相关分量。在实践中,滑行测试不够准确,无法检测到这种影响。因此,滑行测试确定了两个阻力参数。这与在风洞中测量的空气阻力不同,因为它包括向前运动的空气阻力和车轮旋转的空气阻力。表达这些力的更一般的方式是零阶力和二阶力,指的是它们变化的速度的力量。理论上,也可以识别一阶力,其中可能包括轴承摩擦的速度相关分量。在实践中,滑行测试不够准确,无法检测到这种影响。因此,滑行测试确定了两个阻力参数。表达这些力的更一般的方式是零阶力和二阶力,指的是它们变化的速度的力量。理论上,也可以识别一阶力,其中可能包括轴承摩擦的速度相关分量。在实践中,滑行测试不够准确,无法检测到这种影响。因此,滑行测试确定了两个阻力参数。表达这些力的更一般的方式是零阶力和二阶力,指的是它们变化的速度的力量。理论上,也可以识别一阶力,其中可能包括轴承摩擦的速度相关分量。在实践中,滑行测试不够准确,无法检测到这种影响。因此,滑行测试确定了两个阻力参数。
计算功率的第一步是确定阻力系数。在最简单的情况下,这意味着单个阻力区域和单个滚动阻力系数。然后将计算克服每个阻力所需的总功率,这些总和将是所需的总功率。
对于给定的输入功率,可以通过重新排列功率方程来计算自行车速度。为此,必须首先将取决于速度的阻力代入功率方程。不依赖于速度的阻力可以继续表示为单独的参数。当重新排列得到的方程以使速度成为主题时,它变得非常复杂。这意味着它几乎没有直观的价值,而且简单地查看功率与速度的关系图通常更有用。然而,对于计算分析,使用这种形式的方程是有意义的。下面给出一个例子:
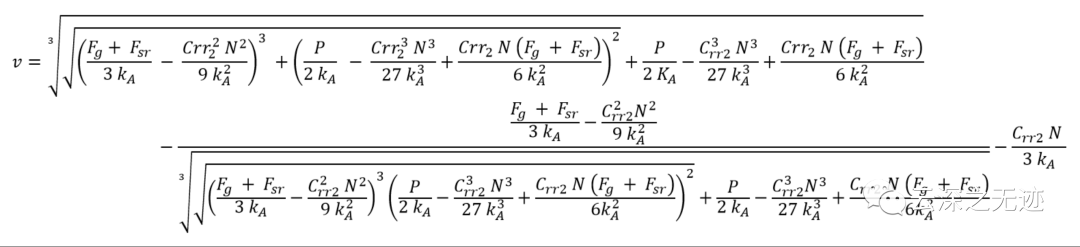
空气阻力实际上与有效迎风面积(EffectiveFrontalArea)、前进速度(Veloity)的平方以及阻力系数(DragCoefficent)成正比。当有效迎风面积增加1倍时,阻力会增加一倍;而阻力系数增加一倍,阻力也会增加一倍;但是速度增加一倍时,阻力则会增加三倍,变成原先的四倍。而在整个自行车运动中,人体所占的有效迎风面积比例最高,风阻系数也较高,产生之空气阻力约 占整体阻力的60%,所以采用低风阻的骑乘姿势对于减小阻力非常有帮助。其次是轮组,因为轮组除了本身在空气中运动的阻力外,钢丝在旋转时亦会产生阻力, 整体轮组约占了整个阻力8%。
https://betterbicycles.org/bicycle-power-calculations/