摘要:
携带轨道角动量(OAM)的电磁波被称为涡旋电磁波,可进一步分为量子态OAM电磁波和统计态OAM电磁波2种。其中,量子态OAM电磁波中每个电磁波量子的内禀OAM不为零,可利用OAM物理量形成无线传输新维度;统计态OAM电磁波则是利用电磁波量子的外部OAM形成具有正交螺旋相位面的统计态波束,由于统计态波束与空域的紧耦合关系,可以被认为是多天线MIMO系统特例。介绍了量子态OAM电磁波和统计态OAM电磁波的传输技术和通信体制,说明了利用OAM维度可超越传统多天线MIMO容量界后形成含有OAM维度的新MIMO容量界。
01
概述
随着信息技术的发展,人们对通信质量提出了更高的要求,针对后5代(B5G)和第6代(6G)移动通信技术的研究已经在全球业界积极展开。欧盟的地平线2020计划(Horizon 2020)对B5G项目进行了资助。美国的联邦通信委员会(FCC)开放了THz频段并早已开始6G研究。芬兰召开了首个6G无线通信全球峰会。国际电信联盟(ITU)则成立了专门的研究小组[1]。在国内,工信部于2019年推动成立了IMT2030推进组[2],旨在推动中国6G通信技术研究,成员包括国内主要运营商和制造商,以及相关高校和研究机构。
一般认为,6G的典型指标包括1 Tbps峰值速率, ![]() 级别延时,数倍于5G移动通信网络的频谱效率等。相对于5G通信网络而言,6G通信网络性能有着显著提升[1]-[5]。为了满足6G需求,业界积极探索新的通信资源和方法,提出了潜在关键技术。其中,轨道角动量(OAM)作为电磁波无线传输新物理维度受到了较为广泛的关注[6]-[10]。
级别延时,数倍于5G移动通信网络的频谱效率等。相对于5G通信网络而言,6G通信网络性能有着显著提升[1]-[5]。为了满足6G需求,业界积极探索新的通信资源和方法,提出了潜在关键技术。其中,轨道角动量(OAM)作为电磁波无线传输新物理维度受到了较为广泛的关注[6]-[10]。
OAM是电磁波的固有物理属性,OAM的物理量纲(ML2T-1)和电场强度的物理量纲(MLT-3I-1)线性无关,所以彼此独立。经典电动力学和量子电动力学(QED)理论均指出,电磁波角动量包括自旋角动量(SAM)和轨道角动量(OAM)[11]。自旋角动量表征了电磁波极化,OAM则表征了电磁波的波包在空间中的旋转特性。具有OAM的电磁波又被称为涡旋电磁波,携带不同OAM模态的涡旋电磁波具备正交特性,利用该特性进行无线传输可以极大地提升频谱效率和传输容量。
OAM可进一步分为内禀OAM(Intrinsic OAM)和外部OAM(Extrinsic OAM)[12]-[15]。电磁波从微观上看是由大量电磁波量子构成的,内禀OAM表征了电磁波量子波包针对其中心形成的OAM,外部OAM则是针对定义的坐标系形成的OAM。因此内禀OAM不会随着外界空间坐标系的不同而发生变化,但外部OAM则会发生相应变化。如果将地月系统比作电磁波量子,则地球自转可表示自旋角动量,月球绕地球公转表示内禀OAM,地月系统绕太阳公转表示外部OAM。
根据主要利用内禀OAM还是外部OAM,涡旋电磁波可分为量子态OAM电磁波和统计态OAM电磁波。量子态OAM电磁波由内禀OAM不为零的涡旋电磁波量子构成;统计态OAM电磁波则是由内禀OAM为零的大量平面电磁波量子统计构建成具有螺旋相位面的涡旋波束形成,其实质上利用的是电磁波量子的外部OAM。
量子态OAM电磁波不能采用传统天线(阵列)产生,需要通过专用装置产生和检测涡旋电磁波量子所携带的OAM模态。量子态OAM电磁波的理论基础主要为量子力学和量子电动力学。由于利用的是电磁波量子的内禀OAM,量子态OAM本质地反映了涡旋电磁波的OAM物理特性,可利用OAM物理量形成无线传输新维度,大幅提高频谱效率,是从电磁波(光波)OAM被提出以来最重要的研究目标。
统计态OAM电磁波可由OAM专用天线或天线阵列产生。因为传统天线只能辐射平面电磁波量子,形成平面波(球面波),所以微观上看统计态OAM电磁波是由大量不同相位的平面电磁波量子构造出的具有正交螺旋相位面的波束,如图1所示,即统计意义上的合成波束,其理论基础主要来源于经典电动力学。统计态OAM电磁波发送和接收都是利用天线,所以直接测量的还是电磁波的电场强度,并不是OAM。只能通过电场强度来间接计算OAM模态,造成统计态波束与空域的紧耦合,没有真正体现出OAM所具备的物理新维度特性。因此,对于统计态OAM电磁波,一直有观点认为其可以被视为多天线MIMO的特例[17],[18]。
本文概述了电磁波OAM传输技术发展历史,强调了量子态OAM电磁波和统计态OAM电磁波概念内涵的差别,介绍了基于量子态OAM电磁波和统计态OAM电磁波传输技术和通信体制,讨论了相应的信道容量,明确了涡旋电磁波OAM传输技术的主要优点。
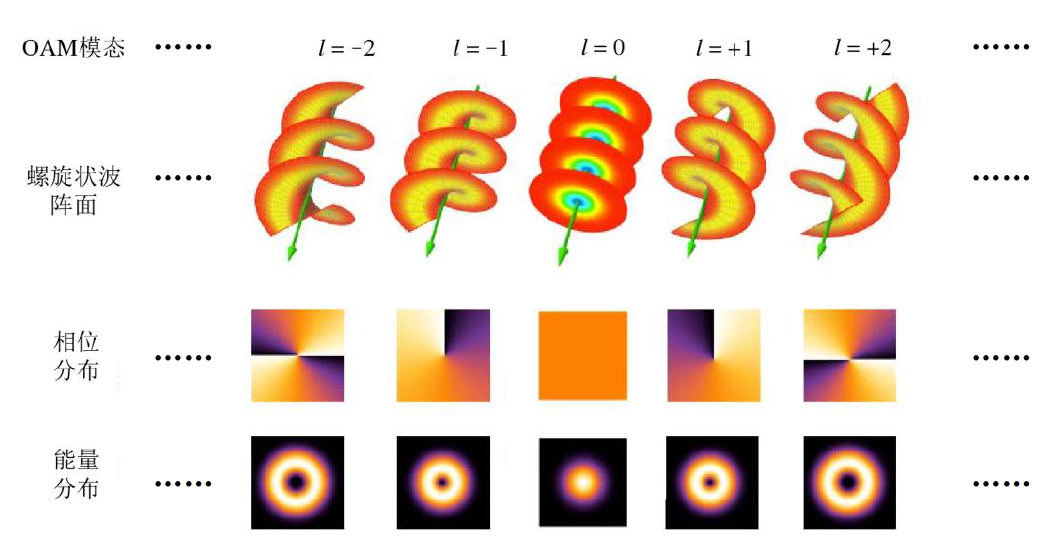
图1 涡旋电磁波相位面及其能量分布[19],[20]
02
OAM传输技术发展历史
OAM最初主要被发现和应用于光学领域,即产生涡旋光子和涡旋光束。1989年,Coullet等人首次提出了涡旋光束的概念[21]。1992年,Allen等人理论证实了涡旋光束中存在OAM[22],并在1994年进行了实验佐证,利用光纤传输OAM光束,实现了1.1 km,1.6 Tbit/s的光信息传输[23]。2011年,Bozinovic等人通过2路OAM光束复用的方式,实现了0.9 km的光纤传输,且模态间串扰小于20 dB[24]。2012年,该课题组在1.1 km长度的光纤中实现了400 Gbps 速率的QPSK调制的OAM模式复用传输实验,信道串扰小于-14.8 dB,多径干扰小于-19.7 dB[25]。2015年,Allen课题组采用键控调制进行传输(QPSK调制,4个OAM模态),传输速率达100 Gbps[26]。
在射频OAM电磁波传输研究方面,1909年Poynting发现电磁波具有角动量,并可以分为自旋角动量和轨道角动量[27]。1996年,Turnbull借鉴光学OAM波产生方法,利用螺旋相位板(SPP)在毫米波段产生了OAM电磁波[28]。2007年瑞典空间物理研究所B. Thidé等人采用均匀环形阵列天线(UCA)对各阵子馈送不同相位,验证了同样可以产生携带轨道角动量的低频电磁波(频率低于1 GHz)[29]。2011年,意大利Fabrizio Tamburini等人设计了OAM螺旋反射面天线,在2.4 GHz频点实现了对电磁波OAM的产生与测量[30],在442 m的威尼斯湖面上完成了2路不同OAM电磁波的传输实验(DVB-S数字视频信号和FM音频信号)[31]。2013年,Mahmouli F. E.等人采用螺旋相位板和全息幅度板2种方式设计了60 GHz频点的OAM天线,并在400 mm距离上实现了4 Gbps视频信号的传输[32]。2014年,Yan Y.等人利用全空域接收方法在2.5 m距离复用传输8路28 GHz频点信号(4种OAM模式且每种模式2种极化),传输速率达到32 Gbps[33]。2015年,Rossella G.等人基于环形天线阵在40 m距离传输了2路VHF波段的视频信号[34]。
近年来,国内科研机构也逐步开展了对涡旋电磁波传输与通信的研究。2016年,浙江大学章献民课题组在构造螺旋相位板的同时加入了透镜设计,降低了OAM电磁波的波束发散角,并通过实验验证了该方法的有效性[35]。次年,该课题组在10 m距离传输了4路10 GHz频点的OAM信号。后续该课题组详细推导了环形行波谐振腔产生涡旋电磁波的天线设计方法,并进行了实验验证。2016年,清华大学航空宇航电子系统实验室(航电实验室)张超团队采用变换域思想,通过旋转发射端的方式将OAM拓扑荷测量转化为电磁波频偏测量[36]。2017年,进一步提出了接收端虚拟旋转方法以完成对OAM模态的检测。该实验室在2016年成功完成微波频段涡旋电磁波27.5 km传输实验[37],并在此基础上于2018年完成了机载172 km传输实验[38]。2018年,南京大学冯一军设计了反射型超表面用于产生OAM涡旋场,利用超表面相位调制特性,实现了工作在Ku波段可以产生特定锥角和OAM模态的超表面反射阵列[39]。
量子态OAM电磁波的研究大都集中在微波频段。由于单个微波量子能量远小于单个光量子,甚至在室温条件下也远小于环境噪声,因此微波量子的研究难度相对较大,尤其是针对单个微波量子的情形[40]。直到2007年,Houck A.等人在低温超导电路中完成了单个微波量子的产生和检测[41]。2016年,美国科罗拉多大学在超低温环境下(<4 K)使用传输和操控了单个微波量子。对于量子态微波的产生,2014年,欧洲Porject8工作组完成单电子回旋加速器辐射实验,得到具有离散能量分布特性的电磁波,验证了单电子回旋加速器辐射量子特性[42]。此外Sawant A.等人在2017年通过仿真及实验证明了回旋行波管中的相对论回旋电子束可以产生具有高阶OAM的微波[43]。日本分子科学研究所的Katoh M.等人分别用理论和实验证明波荡器中的相对论回旋电子能辐射出涡旋电磁波[44],[45]。2019年,Bogdanov O.等人分别基于经典电动力学和量子电动力学理论推导了磁场中相对论电子辐射的频谱分布和OAM谱分布[46]-[48]。2020年清华大学航电实验室分析了OAM在涡旋电子辐射和耦合涡旋微波量子时的转移过程[49]。通过理论推导说明在相对论情形下,由涡旋电子所携带的OAM可以在磁场中转移到微波量子上,从而形成涡旋微波量子。与之相反,在一定条件下涡旋微波量子所携带的OAM也可以转移到与之耦合的电子上,从而形成涡旋电子。2021年,清华大学航电实验室完成了相应的量子态OAM电磁波传输实验。
03
量子态OAM电磁波与统计态OAM电磁波概念内涵的区别
电磁波携带的角动量分为自旋角动量和轨道角动量,可以表示为:
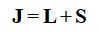
(1)
式中:
J——总的角动量
L——轨道角动量
S——自旋角动量,表征电磁波的极化
根据电动力学理论,可以计算推导得到电磁波所具有的OAM为:
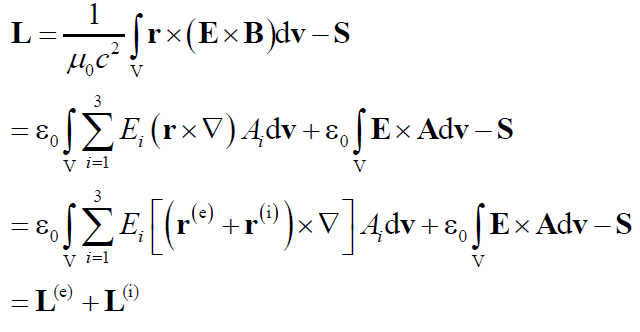
(2)
式中:
![]() ——真空磁导率
——真空磁导率
![]() ——真空介电常数
——真空介电常数
c——真空光速
r——空间坐标
E——电场强度
B——磁场强度
A——磁矢量势
V——积分空间(电磁波所存在的空间)
dv——空间微元
![]() ——电磁波量子内部轨道原点到参考坐标系距离矢量、空间任意一点到内部轨道原点距离矢量,两者之和即是总的位置矢量
——电磁波量子内部轨道原点到参考坐标系距离矢量、空间任意一点到内部轨道原点距离矢量,两者之和即是总的位置矢量
由式(2)可以看到电磁波的OAM与其积分空间、电场强度和磁场强度有关。
根据式(2),电磁波携带的OAM可以分为2个部分,一个是随外界坐标的选取而发生变化的外部轨道角动量![]() ,另一部分则是不随外界坐标选取而变化内禀轨道角动量
,另一部分则是不随外界坐标选取而变化内禀轨道角动量![]() 。具备内禀OAM的电磁波量子称为“涡旋电磁波量子”(比如在微波频段,称为“涡旋微波量子”),由此组成的电磁波便是量子态OAM电磁波。由此可得,量子态OAM电磁波与统计态OAM电磁波最大的区别在于,组成量子态OAM电磁波的电磁波量子是携带内禀轨道角动量的涡旋电磁波量子。在微观层面上,即使单个电磁波量子也具有内禀OAM。而统计态OAM电磁波只是利用了电磁波量子的外部OAM,需要借助宏观的波束赋型,由大量不同相位的平面电磁波量子构造生成具有螺旋相位面的波束,正交模态的波束需要共轴传输。由于统计态OAM电磁波基本用天线产生和接收,所以组成波束的电磁波量子实际上还是平面电磁波量子,而不是涡旋电磁波量子。
。具备内禀OAM的电磁波量子称为“涡旋电磁波量子”(比如在微波频段,称为“涡旋微波量子”),由此组成的电磁波便是量子态OAM电磁波。由此可得,量子态OAM电磁波与统计态OAM电磁波最大的区别在于,组成量子态OAM电磁波的电磁波量子是携带内禀轨道角动量的涡旋电磁波量子。在微观层面上,即使单个电磁波量子也具有内禀OAM。而统计态OAM电磁波只是利用了电磁波量子的外部OAM,需要借助宏观的波束赋型,由大量不同相位的平面电磁波量子构造生成具有螺旋相位面的波束,正交模态的波束需要共轴传输。由于统计态OAM电磁波基本用天线产生和接收,所以组成波束的电磁波量子实际上还是平面电磁波量子,而不是涡旋电磁波量子。
04
OAM电磁波传输技术和通信体制
4.1 量子态OAM电磁波
本节以微波频段为例介绍量子态OAM电磁波的产生和接收检测以及应用场景。
文献[49]分析了OAM在涡旋电子和微波量子的转移过程,通过理论推导说明相对论情形下,OAM可以在涡旋电子和微波量子之间通过磁场中相互作用进行转移。提出可以在相对论效应下利用位于磁场中携带OAM的回旋电子辐射出携带OAM的涡旋微波量子,从而产生量子态OAM电磁波。与之相关的,在前文中提到的Sawant A.等通过用回旋行波管中的相对论回旋电子束在94.8 GHz和98.6 GHz频点分别产生了OAM模态数为5和9的OAM电磁波。日本分子科学研究所的Katoh M.等人分别用理论和实验证明波荡器中的相对论回旋电子能辐射出OAM电磁波。
对于量子态OAM电磁波的接收检测,由于组成量子态OAM电磁波的是涡旋微波量子,可以利用OAM在涡旋微波量子与电子间的转移过程。在接收端布置磁场,使OAM从涡旋微波量子上转移到电子上形成涡旋电子,继而对涡旋电子进行检测便可以实现对OAM模态的识别和分离。
对于涡旋电子的检测问题,其中一种方式为通过衍射图像对其所携带的OAM模态进行分类识别。文献[50]提出了采用单晶和多晶结构薄膜,在磁场中对涡旋电子所携带的OAM模态进行检测。不同的OAM模态将会形成不同的衍射图像(如图2(b)),通过对衍射图像的观测可以实现对OAM模态的识别。其中多晶结构薄膜配合涡旋电子分选器可以用来实现复用OAM模态的检测分离。根据计算,该方法可以在厘米级的宏观尺度上实现对不同OAM模态涡旋电子的识别和分离,易于实现工程应用。
Vincenzo Grillo等人则基于OAM涡旋电子束与磁性物质相互作用的机理,提出并设计实现了一种基于纳米尺度的衍射光栅全息图装置以实现对涡旋电子束携带OAM模态成分的测量[64]。该实验产生了OAM模态从-10到10的涡旋电子束,并用所设计的装置对该电子束的OAM模态成分进行了检测和分析。
2018年,兰州中科院近代物理研究所相应研究团队通过理论分析得出在磁场中携带OAM的涡旋电子将会受到力的作用,且携带不同OAM的涡旋电子束在磁场中的受力情况不同,因而加速度也不相同,从而具备不同的速度和运动轨迹,因此可以增加一个横向磁场,并利用速度选择器对携带不同OAM的涡旋电子束进行分离[65]。如图2(d)所示。
量子态OAM电磁波传输通过涡旋微波量子的产生和检测进行通信,可以直接检测涡旋微波量子所携带的OAM模态。而量子态OAM电磁波经过反射、散射等情况后其所携带的OAM模态数绝对值不变,因此可以适用于视距与非视距、近距离与长距离等各种场景。
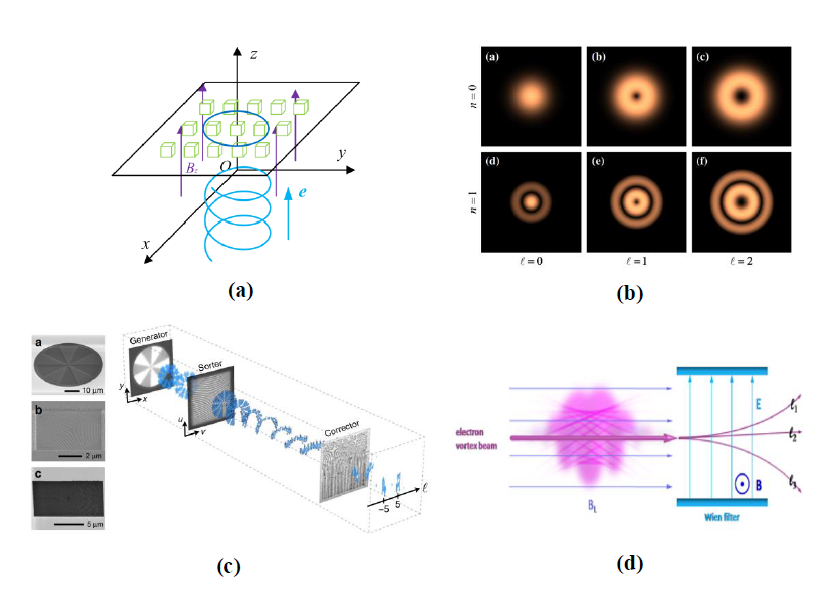
图2:(a)涡旋电子在磁场中被晶体的晶胞所散射[50];(b)不同OAM涡旋电子经过晶体后的分布情况[50];(c)涡旋电子衍射光栅全息图分选装置[64];(d)涡旋电子速度分选装置[65]
4.2 统计态OAM电磁波
由于统计态OAM电磁波可以采用天线(阵列)发射和接收,所以发展较早且技术较成熟。下面主要介绍统计态OAM电磁波的产生和接收方法以及应用场景。
统计态OAM电磁波的产生方法主要有以下5种。
a)螺旋相位板方式。螺旋相位板产生统计态OAM电磁波的原理是通过相位板厚度的连续变化构造一个不均匀相位延时结构,如图3(a)所示。当平面波通过螺旋相位板时,由于不同位置的厚度和延时不一样,平面波产生连续变化的相位,从而形成螺旋相位面波前[32],[52]。该方式优势在于波束发散小和衰减低。缺点是设计定型后,其产生的OAM模态单一固定,不能进行改变。
b)螺旋反射面天线方式。螺旋反射面天线方式指的是通过将普通抛物面天线通过开槽等方式扭曲加工成螺旋状的反射面,如图3(b)所示。当电磁波通过螺旋反射面天线发射时,由于其螺旋状的反射面形状将会使发射的电磁波具有螺旋相位波前,通过调整相应参数可以获得相应模态的统计态OAM电磁波[53]。
c)衍射光栅方式。衍射光栅方式通过由平行细缝组成的光学结构对入射波进行衍射,形成衍射波, 如图3(c)所示。然后通过入射波和衍射波之间的干涉从而形成具备螺旋相位的统计态OAM电磁波[32],[51]。
d)阵列天线方式。阵列天线产生统计态OAM电磁波的基本原理是将天线阵列布置成环形形式,然后由不同位置的阵子馈送不同初始相位的平面波。不同阵子发射的具有不同相位的平面波叠加后便可以形成螺旋相位面的涡旋电磁波[29],[54],[55]。调整天线阵子初始相位,便可以产生不同模态的统计态OAM电磁波。比如典型的均匀环形阵列(UCA)方式,如图3(d)所示,其优点在于不需要复杂的天线设计,实现原理相对简单。
e)超表面方式。超表面是一种超薄的二维阵列表面,由亚波长大小周期性排列的超材料谐振单元组成,它可以通过改变谐振单元的形状和大小等参数来实现电磁波振幅或相位上的变化,如图3(e)所示,因此可以应用于统计态OAM电磁波的产生[59]-[61]。超表面天线具有剖面低、馈电系统简单和易于波束成形等优点。目前用于产生OAM波的超表面天线可分为4类:反射型超表面、透射型超表面、全息超表面和数字编码型超表面。
在以上几种统计态OAM电磁波的产生方式中,螺旋相位板、螺旋反射面、衍射光栅方式是专为产生具备螺旋相位面的OAM电磁波而设计,可以称之为OAM专用天线。而阵列天线、超表面方式则本质上是天线的不同排布方式,属于天线阵列。
统计态OAM电磁波的接收检测方法主要有:
a)全相位面共轴接收。基本原理是在接收端采用的天线或天线阵列覆盖完整的相位面,共轴传输成为多模态复用和解复用的关键,非对准情况下模态间干扰会很大。比如发送端采用螺旋相位面板,则接收端采用与之厚度变化趋势相反的螺旋相位面板,覆盖全相位面,使螺旋相位面恢复成平面波,也可以在接收端使用UCA天线[19]。
b)部分相位面接收。即根据不同OAM模态的电磁波在天线间距相同的情况下相位差与模态数有关的原理,在接收端的环形相位面上布置天线阵列覆盖部分弧段,完成对相位差的检测继而实现对不同OAM模态检测和分离[19],[63]。由于涡旋波束为倒锥状发散波束,所以该方法适用于涡旋波束的长(远)距离无线传输。
统计态OAM电磁波的波束呈倒锥状,而倒锥状波束导致传输距离越长波束越发散,容量和距离产生矛盾。全相位面接收可支持大容量传输,但基本应用于近距离点对点场景,比如6G中宏基站到微基站的中继传输;部分相位面支持长距离传输,但是传输容量会随部分相位面的比例下降。
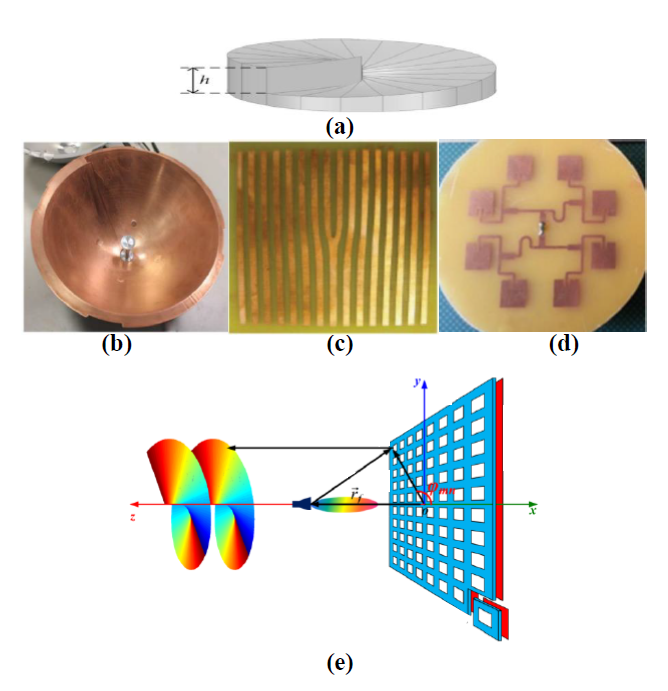
图3:(a)螺旋相位面板[32];(b) 螺旋反射面[53];(c)衍射光栅[32];(d)均匀环形阵列[56];(e)超表面结构[58]
05
量子态与统计态OAM电磁波传输信道容量分析
根据所使用的OAM传输技术,可以将其信道容量分为4个区域[66]。
首先是采用量子态OAM电磁波进行传输。直接通过产生和检测OAM涡旋微波量子进行通信,而OAM是独立于电场强度等传统物理量之外的新维度,因此传输的信道容量可以超过传统多天线MIMO的信道容量上界。该种方式对应于图4中的A区域。其上界为包含OAM维度的新MIMO容量界。
其次是统计态OAM电磁波传输中采用专用OAM天线。统计态OAM专用天线包括螺旋相位板、螺旋反射面、衍射光栅等。OAM专用天线不同与传统多天线MIMO,可以改变点对点传输信道。比如采用螺旋抛物面天线等统计态OAM专用天线用于视距(Line of Sight, LoS)传输信道,改善了由于信道相关所带来的传输信号降秩问题,容量接近于传统多天线MIMO系统的容量上界。该种方式对应于图4中的B区域。
其三是统计态OAM电磁波传输中不使用特殊天线,而是采用UCA等天线阵列方式进行发送和接收,此时明显可以将其视为MIMO系统的特例。在LoS信道下,天线阵列OAM电磁波传输方式的信道容量介于开环LoS-MIMO系统和闭环LoS-MIMO系统的信道容量之间。该种方式对应于图4中的C区域,仅具有复杂度的优势。
最后是在长(远)距离传输场景下,采用部分相位面接收检测时,OAM模态难以被正交分离,信道容量将会低于开环LoS场景下的MIMO容量界,对应图4中的D区域。
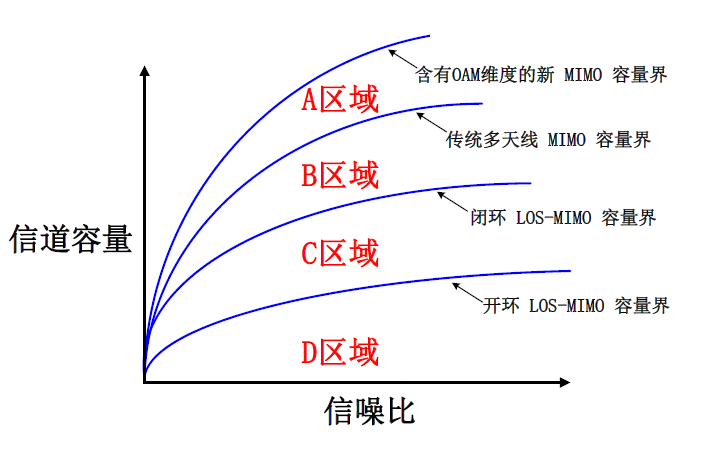
图4:典型OAM传输技术信道容量区域
划分示意图[67].
06
总结与展望
本文介绍了6G中的潜在核心关键技术——涡旋电磁波轨道角动量传输技术,包括:简要综述了涡旋电磁波的发展历史,明确了统计态OAM电磁波和量子态OAM电磁波的概念和区别,列举了2种OAM电磁波传输技术对应的产生和接收检测方法以及其应用场景,并对典型OAM传输技术进行了信道容量分析。说明了利用OAM维度,可超越传统多天线MIMO容量界后形成含有OAM维度的新MIMO容量界。
对于统计态OAM电磁波而言,其波束呈倒锥状,仅能用于点对点LoS环境传输,且面临长距离传输后波束发散问题,该问题极大地限制了统计态OAM波束在通信方面的应用。如果能提出相应方法实现统计态OAM电磁波的波束汇聚,解决统计态OAM电磁波长距离波束发散这一问题,将会大大拓展OAM电磁波通信的应用场景。
对于量子态OAM电磁波而言,其调控装置的小型化是关键问题。目前量子态OAM涡旋电磁波的产生需要用到强磁场、真空电子器件等设施条件,导致量子态OAM调控装置往往过于庞大和冗重,限制了应用场景。因此如何能有效地将量子态OAM电磁波的调控装置小型化,是个颇具价值的研究方向,也是量子态OAM电磁波走向工程实用的关键。
参考文献
[1]Zhengquan Zhang, Yue Xiao, Zheng Ma, Ming Xiao, Zhiguo Ding, Xianfu Lei, George K. Karagiannidis, Pingzhi Fan. 6G wireless networks: vision, requirements, architecture, and key technologies[J]. IEEE Vehicular Technology Magazine, 2019, 14(3).
[2]IMT-2030(6G)推进组. 6G总体愿景与潜在关键技术[EB/OL]. http://www.caict.ac.cn/kxyj/qwfb/ztbg/202106/P02021060455257-2072895.pdf, 2021.
[3]You Xiaohu, Wang Cheng Xiang, Huang Jie et.al. Towards 6G wireless communication networks: vision, enabling technologies, and new paradigm shifts[J]. Science China Information Sciences, 2020, 64(1).
[4]张平,牛凯,田辉,聂高峰,秦晓琦,戚琦,张娇.6G移动通信技术展望[J].通信学报,2019,40(01):141-148.
[5]赵亚军,郁光辉,徐汉青.6G移动通信网络:愿景、挑战与关键技术[J].中国科学:信息科学,2019,49(08):963-987.
[6]Vahidinia Vahideh, Atashbar Mahmoud, Hosseinzadeh Shahram. Orbital angular momentum and mode multiplexing based index modulation[J]. Physical Communication,2021,48.
[7]Al Amin, Ahmed, Shin, Soo Young. Capacity analysis of cooperative NOMA-OAM-MIMO based full-duplex relaying for 6G[J]. IEEE Wireless Communications Letters, 2021, 10(7):1111395-1399.
[8]Lee SangHoon, Al Amin Ahmed, Shin SooYoung. Orbital angular momentum-based multiple-input-multiple-output with receive antenna shift keying for 6G[J]. Electronics, 2021, 10(13).
[9]Huang Shanguo, Song Xiyao, Gao Xinlu, Zheng Zhennan, Cao Zizheng, Ma Jingcan, Bai Yunping, Koonen A M J. Analog radio of fiber link of 2-Gbaud OOK/BPSK radio frequency-orbital angular momentum beam transmission over 19.4 km[J]. Optics express, 2021, 29(2).
[10]Jin Jiang, Chao Zhang. Orbital angular momentum beamforming based on multi-loop uniform circular array with interferometry codes: Regular Section[J]. IEICE Communications Express, 2021, 10(8).
[11]Jackson J D. Classical Electrodynamics[M]. New York: Wiley Press, 1999.
[12]Harris J, Grillo V, Mafakheri E, et al. Structured quantum waves[J]. Nature Physics, 2015, 11(8):629.
[13]Oemrawsingh S S R, Eliel E R, Nienhuis G, Woerdman J P. Intrinsic orbital angular momentum of paraxial beams with off-axis imprinted vortices[J]. Journal of the Optical Society of America. A, Optics, image science, and vision, 2004, 21(11).
[14]A. T. O’Neil, I. MacVicar, L. Allen, and M. J. Padgett. Intrinsic and extrinsic nature of the orbital angular momentum of a light beam[J]. Physical review letters, 2002, 88(5).
[15]邓锡铭,盛国平.电磁场的内禀角动量[J].中国激光,1990(07):394-406.
[16]ZHANG Chao, JIANG Jin, and ZHAO Yufei. Euclidean space with orbital angular momentum[C]. 2019 IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 2019:1–6.
[17]EDFORS O and JOHANSSON A J. Is orbital angular momentum (OAM) based radio communication an unexploited area[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(2):1126–1131.
[18]Tamagnone M, Silva J S, Capdevila S, et al. The orbital angular momentum (OAM) multiplexing controversy: OAM as a subset of MIMO[C]. 2015 9th European Conference on Antennas and Propagation (EuCAP), Lisbon, Portugal, 2015: 1–5.
[19]马路. 电磁波轨道角动量长距离传输方法研究[D]. 清华大学,2017.
[20]Wikipedia. Orbital angular momentum of light [EB/OL]. (2016-11-31) [2017-03-30] https://en.wikipedia.org/wiki/Orbital_angular_momentum_of_light
[21]P. Coullet, L. Gil, F. Rocca. Optical vortices. Optics Communications 1989,73(5):403-408.
[22]Allen L, Beijersbergen M W, Spreeuw R J and Woerdman J P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Physical Reviewer A, 1992, 45(11):8185-8189.
[23]Barnett S M, Allen L. Orbital angular momentum and nonparaxial light beams[J]. Optics Communications, 1994, 110:679-688.
[24]Bozinovic N, Kristensen P, Ramachandran S. Long-range fiber-transmission of photons with orbital angular momentum[J]. IEEE Lasers and Electro-Optics, 2011, 47(10):1-2.
[25]Bozinovic N, Yue Y, Ren Y, et al. Orbital angular momentum (OAM) based mode division multiplexing (MDM) over a km-length fiber[C]. European Conference and Exhibition on Optical Communication, 2012.
[26]Willner A J, Ren Y, Xie G, et al. Experimental demonstration of 20 Gbit/s data encoding and 2 ns channel hopping using orbital angular momentum modes[J]. Optics Letters, 2015, 40(24):5810.
[27]Poynting J H. The wave motion of a revolving shaft, and a suggestion as to the angular momentum in a beam of circularly polarised light[J]. Proceedings of the Royal Society A, 1909, 82(557):560-567.
[28]Turnbull G A, Robertson D A, Smith G M, et al. Generation of free-space Laguerre-Gaussian modes at millimetre-wave frequencies by use of a spiral phase plate[J]. Optics Communications, 1996, 127(4-6):183-188.
[29]Thidé B, Then H, Sjöholm J, et al. Utilization of photon orbital angular momentum in the low-frequency radio domain[J]. Physical Review Letters, 2007, 99(8):87701.
[30]Tamburini F, Mari E, Bo T, et al. Experimental verification of photon angular momentum and vorticity with radio techniques[J]. Applied Physics Letters, 2011, 99(20):204102-204103.
[31]Tamburini F, Mari E, Sponselli A, et al. Encoding many channels in the same frequency through radio vorticity: first experimental test[J]. New Journal of Physics, 2011, 14(3):811-815.
[32]Mahmouli F E, Walker S D. 4-Gbps Uncompressed video transmission over a 60-GHz orbital angular momentum wireless channel[J]. IEEE Wireless Communications Letters, 2013, 2(2):223-226.
[33]Yan Y, Xie G, Lavery M P J, et al. High-capacity millimetre-wave communications with orbital angular momentum multiplexing[J]. Nature Communications, 2014, 5:4876.
[34]Gaffoglio R, Cagliero A, Vita A D, et al. OAM multiple transmission using uniform circular arrays: numerical modeling and experimental verification with two digital television signals[J]. Radio Science, 2015, 51(6):645-658.
[35]Yiling Chen, Shilie Zheng, Yue Li, Xiaonan Hui, Xiaofeng Jin, Hao Chi, and Xianmin Zhang. A flat-lensed spiral phase plate based on phase-shifting surface for generation of millimeter-wave OAM beam[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15:1156-1158.
[36]Zhang C, Ma L. Millimetre wave with rotational orbital angular momentum[J]. Scientific Report, 2016, 6: 31921.
[37]Chao Z, Lu M A. Detecting the orbital angular momentum of electro-magnetic waves using virtual rotational antenna[J]. Scientific Report, 2017, 7(1):4585.
[38]Zhang C, Zhao Y. Orbital angular momentum nondegenerate index mapping for long distance transmission[J]. IEEE Transactions on Wireless Communications, 2019, 18(11):5027-5036.
[39]Guowen Ding, Ke Chen, Tian Jiang, Boyu Sima, Junming Zhao, Yijun Feng. Full control of conical beam carrying orbital angular momentum by reflective metasurface[J]. Opt. Express., 2018, 26(16):20990-21002.
[40]徐鹏飞. 电磁波轨道角动量量子态研究[D]. 清华大学, 2020.
[41]Houck A A, Schuster DI, Gambetta J M, et al. Generating single microwave photons in a circuit[J]. Nature, 449(7160):328-331.
[42]Asner D M, Bradley R F, De Viveiros L, et al. Single-electron detection and spectroscopy via relativistic cyclotron radiation[J]. Physical Review Letters, 2015,114:162501.
[43]Sawant A, Choe M S, Thumm M, et al. Orbital angular momentum (OAM) of rotating modes driven by electrons in electron cyclotron masers[J]. Scientific Reports,2017,7:3372.
[44]Katoh M, Fujimoto M, Kawaguchi H, et al. Angular momentum of twisted radiation from an electron in spiral motion[J]. Physical Review Letters, 2017,118:094801.
[45]Katoh M, Fujimoto M, Mirian N S, et al. Helical phase structure of radiation from an electron in circular motion[J]. Scientific Reports, 2017, 7:6130.
[46]Bogdanov O V, Kazinski PO, Lazarenko G Y. Semiclassical probability of radiation of twisted photons in the ultra relativistic limit[J]. Physical Review D, 2019, 99:116016.
[47]Bogdanov o V, Kazinski P O, Lazarenko G Y. Probability of radiation of twisted photons by classical currents[J]. Physical Review A, 2018,97:033837.
[48]Bogdanov O V, Kazinski P O, Lazarenko G Y. Probability of radiation of twisted photons in an inhomogeneous isotropic dispersive medium[J]. Physical Review A, 2019,100:043836.
[49]Chao Zhang, Pengfei Xu, Xuefeng Jiang. Vortex electron generated by microwave photon with orbital angular momentum in a magnetic field[J]. AIP Advances, 2020,10:105230.
[50]Chao Zhang, Pengfei Xu, Xuefeng Jiang. Detecting superposed orbital angular momentum states in the magnetic field by the crystal diffraction[J]. The European Physical Journal Plus, 2021,136(60).
[51]Kuang Zhang, Yuxiang Wang, Yueyi Yuan, Shah Nawaz Burokur. A review of orbital angular momentum vortex beams generation: from traditional methods to metasurfaces[J]. Applied Sciences, 2020, 10(3).
[52]Beijersbergen M W, Coerwinkel R P C, Kristensen M, et al. Helical-wave front laser beams produced with a spiral phase plate[J]. Optics Communications, 1994, 112(5/6): 321–327.
[53]Mari Elettra, Spinello Fabio, Oldoni Matteo, Ravanelli Roberto A., Romanato Filippo, Parisi Giuseppe. Near-field experimental verification of separation of OAM channels[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14.
[54]Tennant, A.; Allen, B. Generation of OAM radio waves using circular time-switched array antenna[J]. Electron Letter, 2012, 48:1365–1366.
[55]Tamburini F, Thidé B, Boaga V, et al. Experimental demonstration of free-space information transfer using phase modulated orbital angular momentum radio[J]. Physics, 2013: 1–7.
[56]Bai, Q., Tennant, A.; Allen, B. Experimental circular phased array for generating OAM radio beams[J]. Electron. Lett., 2014, 50.
[57]Bai Q., Tennant A., Allen B., Rehman M.U. Generation of orbital angular momentum (OAM) radio beams with phased patch array[C]. 2013 Loughborough Antennas and Propagation Conference (LAPC), Loughborough, UK, 2013:410–413.
[58]Yu, S.X.; Li, L.; Shi, G.M.; Zhu, C.; Zhou, X.X.; Shi, Y. Design, fabrication, and measurement of reflective metasurface for orbital angular momentum vortex wave in radio frequency domain[J]. Appl. Phys. Lett., 2016, 108, 121903.
[59]Yuan Y, Ding X, Zhang K, et al. Planar efficient metasurface for vortex beam generating and converging in microwave region[J]. IEEE Transactions on Magnetics. 2017, 53(6):2500204.
[60]Liu S, Noor A, Du L L, et al. Anomalous refraction and nondiffractive Bessel-beam generation of terahertz waves through transmission-type coding metasurfaces[J]. ACS Photonics, 2016, 3(10):1968-1977.
[61]刘硕. 基于数字表征的编码超表面及其应用 [D]. 东南大学, 2017.
[62]马路. 电磁波轨道角动量长距离传输方法研究[D]. 清华大学,2017
[63]Zhang W, Zheng S, Chen Y, et al. Orbital angular momentum-based communications with partial arc sampling receiving[J]. IEEE Communications Letters, 2016, 20(7):1381-1384.
[64]Vincenzo Grillo, Amir H. Tavabi, et.al. Measuring the orbital angular momentum spectrum of an electron beam[J]. Nature communications. 2017.
[65]Alexander J. Silenko, Pengming Zhang and Liping Zou. Manipulating Twisted Electron Beams[J]. Physical Review Letters, 2017,119.
[66]赵宇飞.涡旋电磁波长距离大容量传输方法研究[D]. 清华大学,2020.
[67]广东省新一代通信与网络创新研究院. 6G无线热点技术研究白皮书[EB/OL],
https://mp.weixin.qq.com/s/NES2kXc2kjcQnY6Y3Pk0HQ
作者简介:
谢翔东,清华大学航天航空学院硕士研究生,研究方向为涡旋电磁波传输与通信等。
何耀宇,清华大学航天航空学院博士研究生,研究方向为5G航空通信,涡旋电磁波传输等。
张超,清华大学航天航空学院长聘教授,博士,研究方向为涡旋电磁波传输与探测等。
推荐阅读
■ 智能超表面技术5G 化演进探讨
■ 基于效能领先的5G无线覆盖解决方案
■ 运营商AI能力建设及演进探讨
■ 基于信道特性与保守混沌的5G电力物联网动态加密算法

扫描二维码 |关注我们
头条号:邮电设计技术
官方网站:http://ydsjjs.paperopen.com
编辑:李星初 审核:唐艳超