简 介： 本文讨论了傅里叶变换中相互关联的三个性质，时移特性、频移特性和尺度特性。对于信号与系统的理解需要能够在经典理论、物理直观以及数值计算三个方面进行深入挖掘和理解，这样在未来的应用中才能够更好的透过现象看本质。
关键词： FFT，时移特性，频移特性，尺度特性

00 背  景

  今天在  西土城山羊卷^[1] 的博客看到她在其博文 傅里叶变换：时移与频移性质解读｜CSDN创作打卡^[2] 中谈到对于傅里叶变换中的时移和频移的理解。其中两个观点还是蛮有新意的。

01 时移特性

  傅里叶变换的时移特性表明了信号 经过延迟时间   之后，形成信号 。那么它对应的傅里叶变换 与原始信号 对应的频谱 之间的关系为：

1.1 性质证明

  证明这个性质非常容易，只要在傅里叶变换的定义上，通过 变量替换^[2] 便可以在三步之内完成证明。

  根据傅里叶变换定义：

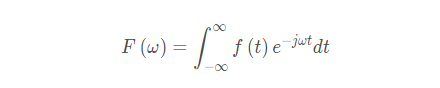
  那么对于：

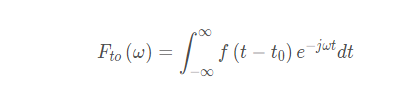
  利用： ，原来表达式可以写为：

1.2 物理解释

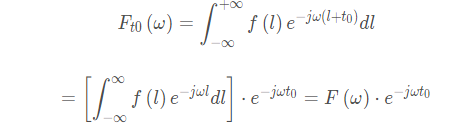
  从上面的公式可以看出两点：

• 由于时间延迟，信号中所有频率分量都出现了一个负相位 因子： ;而信号的幅度谱不变。
• 每个频率的负相位与该频率成线性关系，比例为   。

1.2.1 特定信号举例

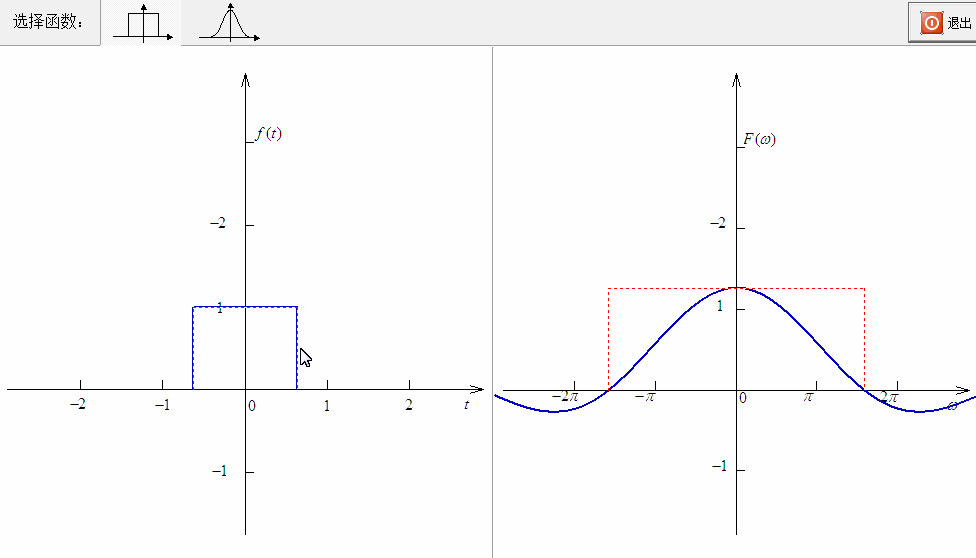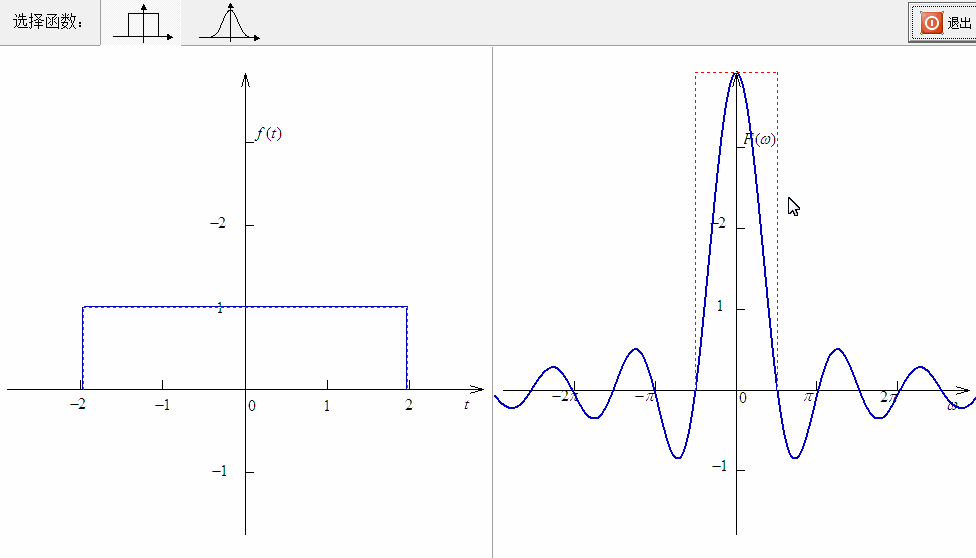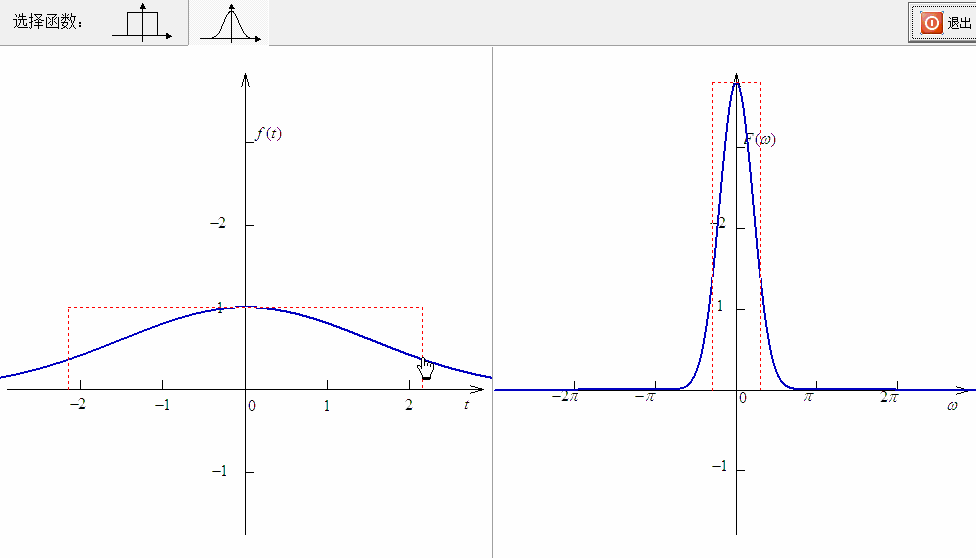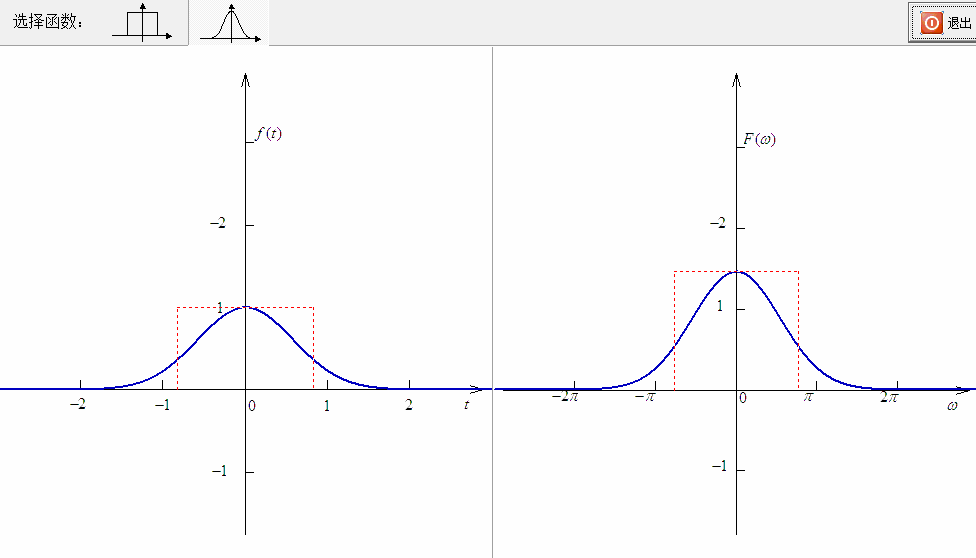
  下面给出一个由四个频率组成的振荡信号：

  它对应的波形为：

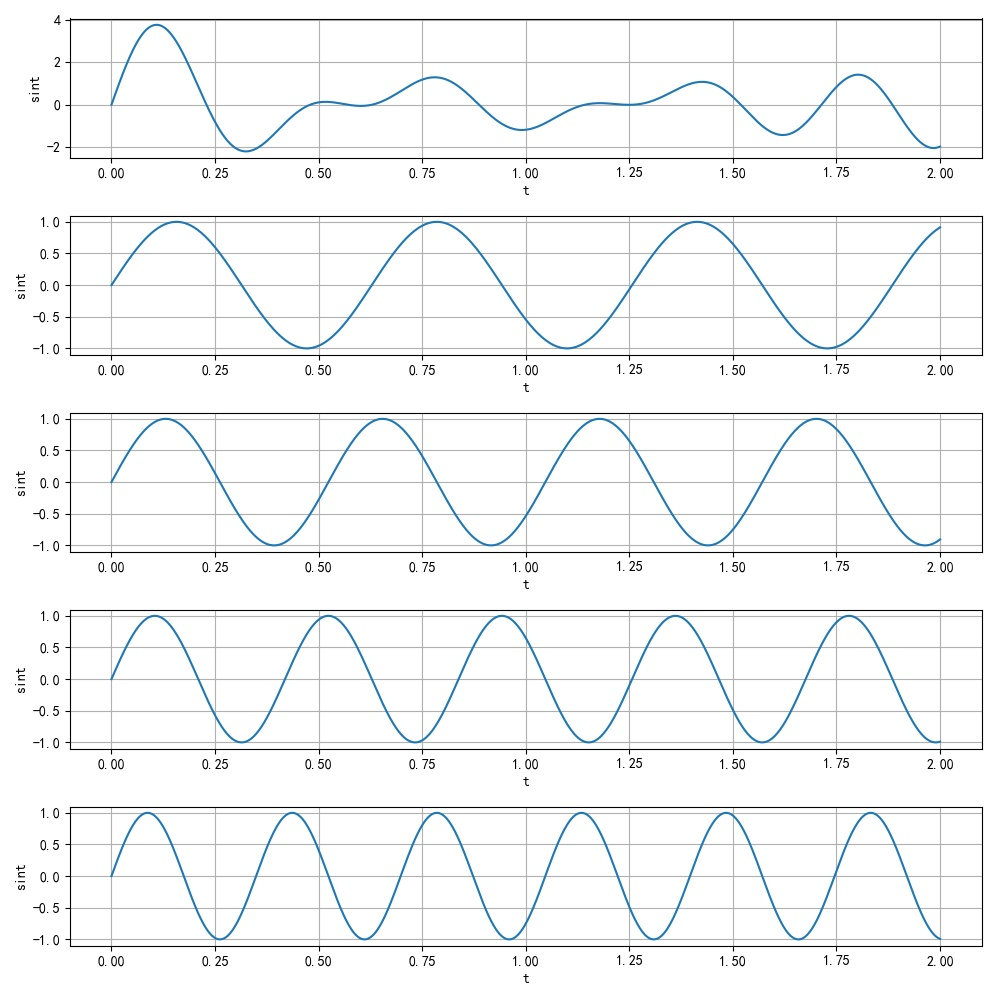
  下面假设信号平移了   ，变成了   。那么对应的波形为：

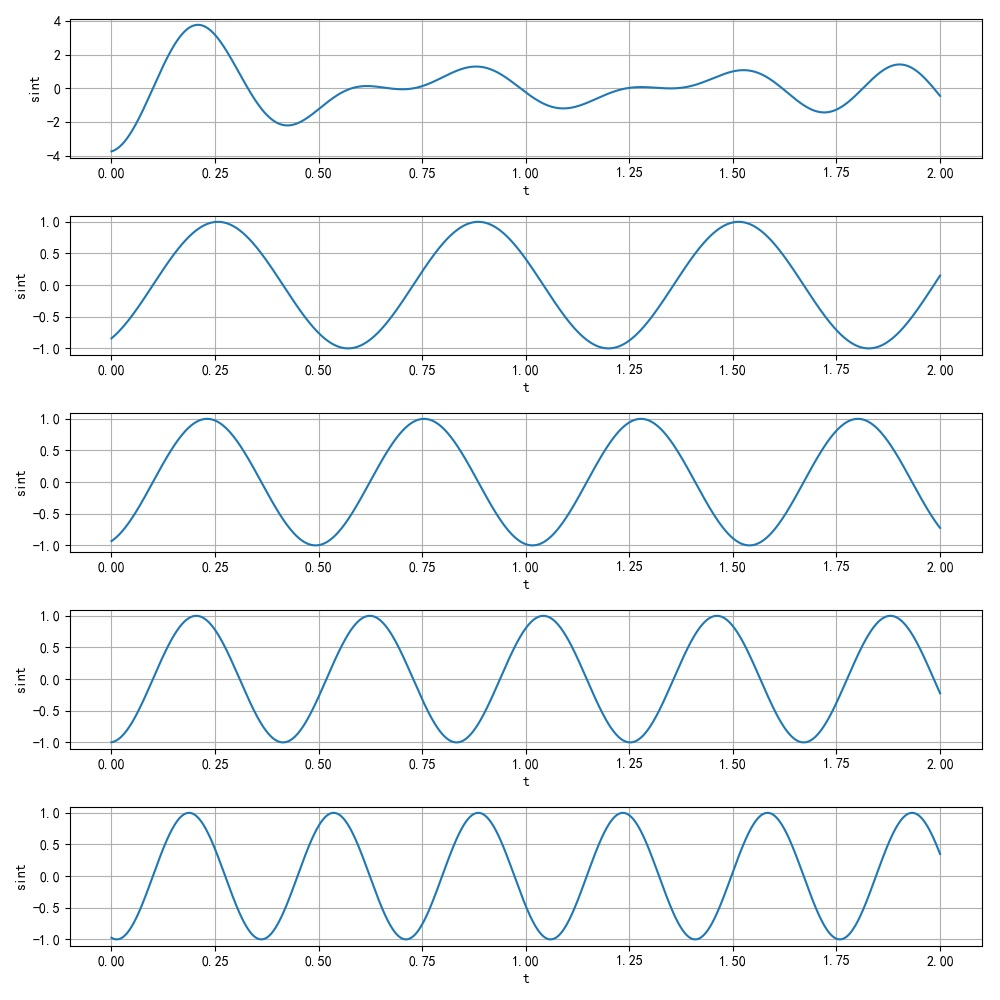
  在上面图中，可以明显看到，原来信号延迟的时间 ，所有频率分量都延迟相同的时间 。在此基础上， 西土城山羊卷^[2] 给出了两点有趣的解释，她认真解释的很到位：

• 为什么对应的延迟时间 时，所有的相位都是负的？从上图中可以直观看到所有的正弦分量的起始点实际上都基本上对应的是负的相位。
• 为什么不同频率对应的相位延迟不同？就是对于相同的时间 ，转换到相位时 与频率成正比。

02 频移特性

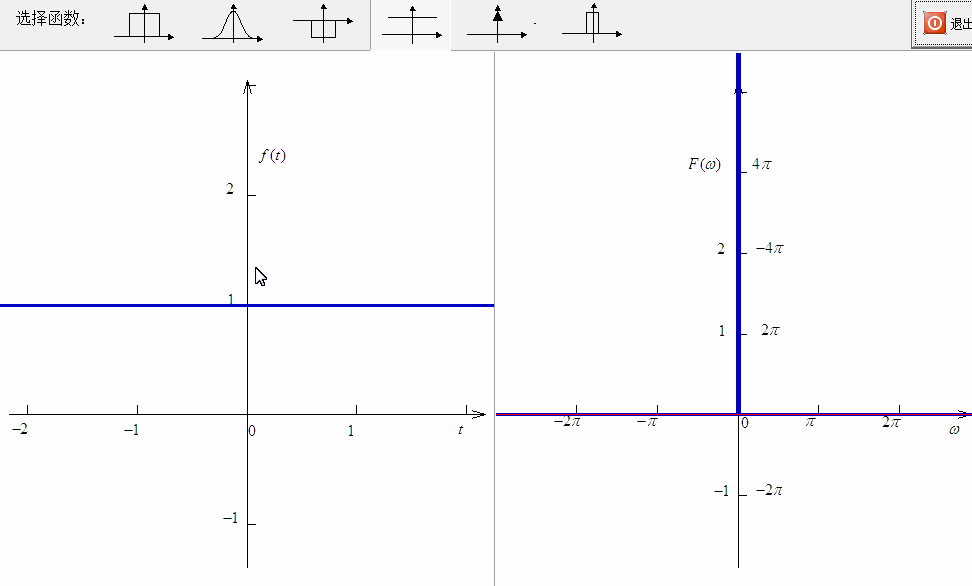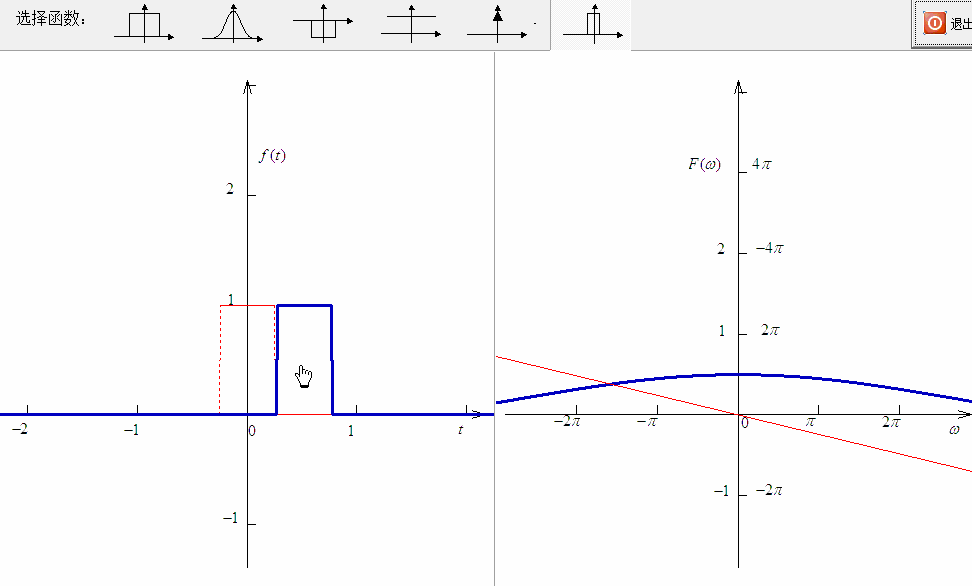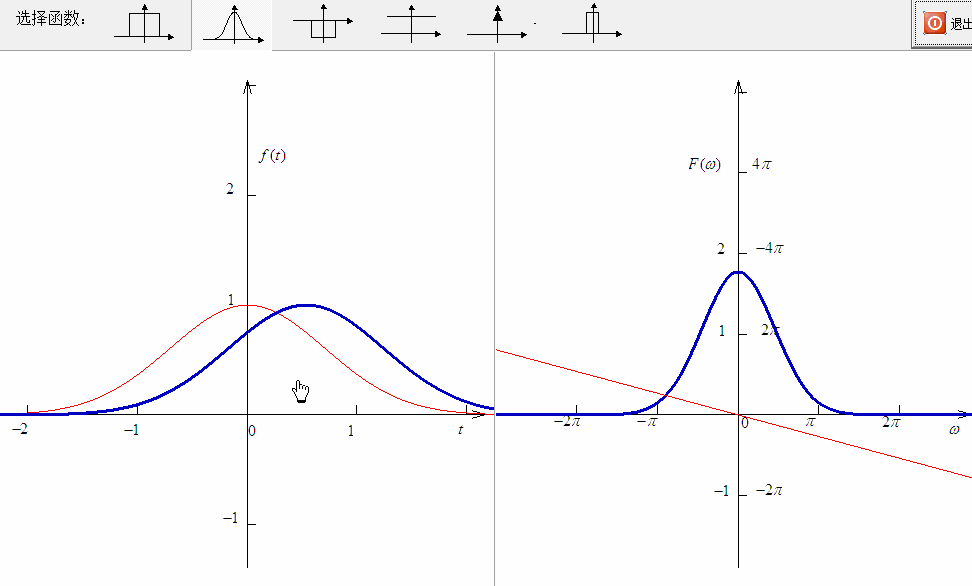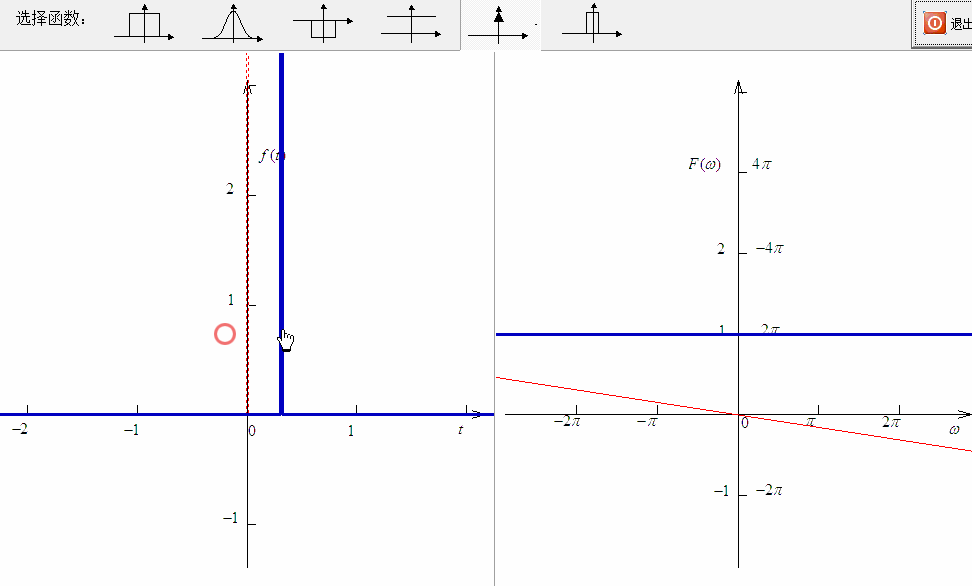
  实际上 西土城山羊卷^[3] 博文中有趣的观点在于对于傅里叶变换频移特性的阐述。

2.1 性质证明

  这是在傅里叶变换中与时移特性对偶的一个特性。它讲述了如果把信号 的频谱 在频域进行平移 ，变成 ，那么对应的时域信号变成：

  对比一下前面的时移特性，你会发现频移特性几乎与时移特性一模一样，只是叙述的时域、频域颠倒了一下，另外在时域信号上增加的相位因子是正的。

  证明过程也与前面时移特性一样，只需要从傅里叶反变换出发，利用变量替换也就可以了。

2.2 物理解释

  但是在实际中，对于频移特性的物理解释则是从时域的角度来阐明。即在时域中，信号 不是被称为增加了一个相位因子，而是指信号 对振荡信号 进行 幅度调制^[4] ，调制后的信号 的频谱是原来信号 的频谱 进行平移。通常情况下，是频谱从低频搬移到高频。

  当然，也可以利用这个原理将信号的频谱从高频搬回到低频。从而实现了信号的调制与解调。

  在通常情况下，对于信号调制都是使用正弦波，而不是复振荡信号，因此对应的信号频谱就表现为左右平移的情况。如下图所示。

2.3 尺度变换对应的频率变化

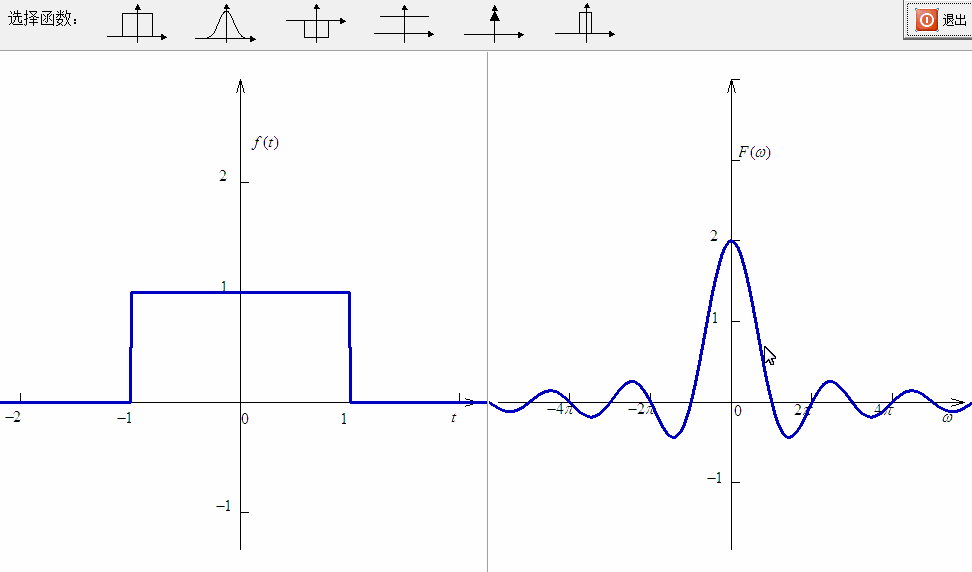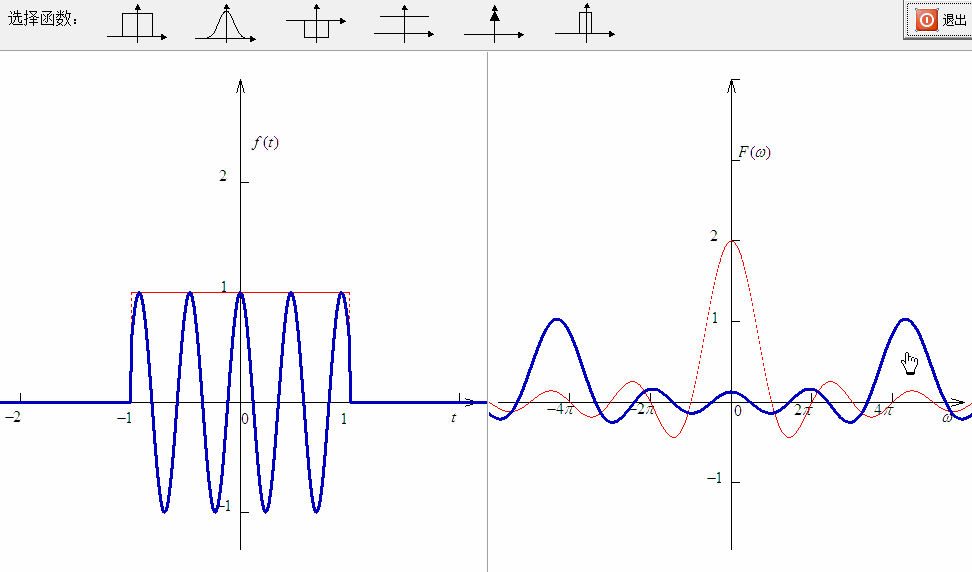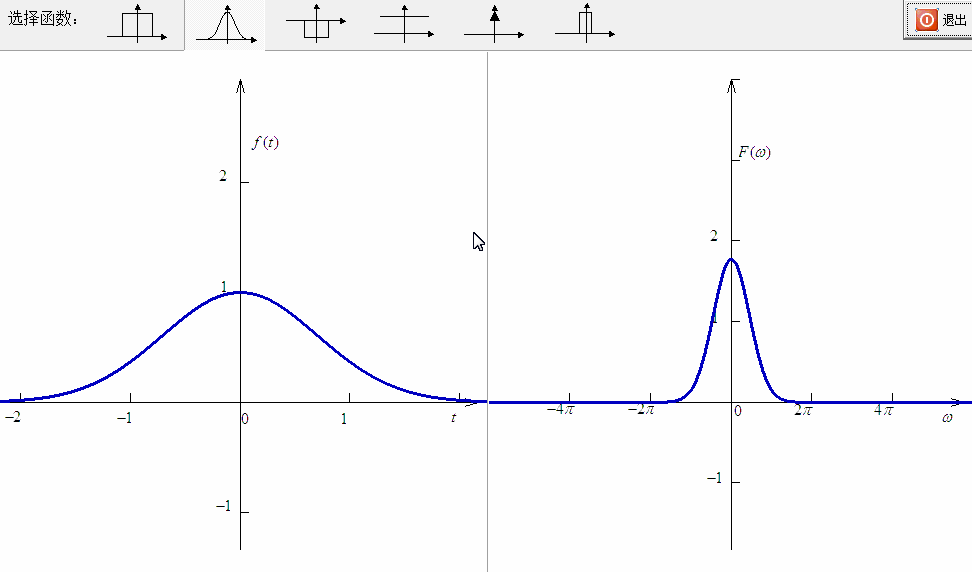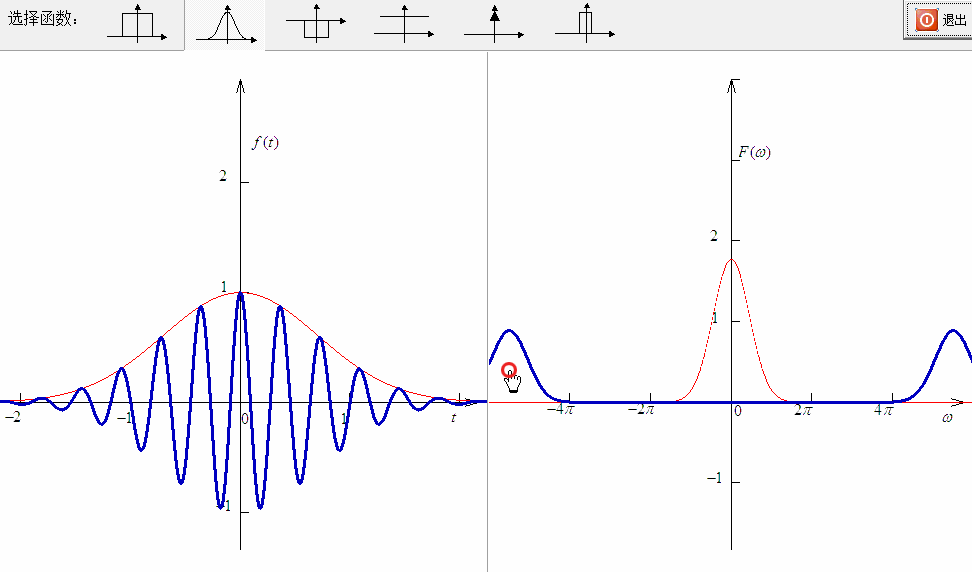
  西土城山羊卷^[2] 在解释信号频谱搬移的时候提出了一个有趣的观点：你看看，信号的频谱搬移到高频了，所有的频率都增加了。为什么信号在时域表现不是尺度变化呢？

  也就是： 。比如， ，对应的 ，这个频率也变高了。

  如果这样考虑，这就会引出傅里叶变换中的“尺度变化”性质。

  如果 一个信号在时域发生了尺度变化 ，这个信号有可能被压缩（    ），也有可能被拉长（ ），这都会引起其中的频率分量的变化。但这个变化不再是平移，而是呈现相反的尺度变化：

  这个规律与频移是不同的。

  在一般的工程应用中，尺度变化实现起来不太容易，但在“空间换时间，时间换空间”的过程中，可以通过巧妙的设置，完成信号在时域和频域中的尺度变换。

※ 变换总结 ※

  本文讨论了傅里叶变换中相互关联的三个性质，时移特性、频移特性和尺度特性。对于信号与系统的理解需要能够在经典理论、物理直观以及数值计算三个方面进行深入挖掘和理解，这样在未来的应用中才能够更好的透过现象看本质。

参考资料