摘要: 在电源芯片的数字控制方法中,经常引入延迟环节。在引入延迟环节后,分析电路响应的方法特别是定量计算会变得比较复杂。本文通过对一种有延迟环节的burst控制方法的分析,提出一种可用于工程实践的方法,那就是通过电路分析,用在静态工作点作瞬态响应仿真的方法得到参数调试方向。
关键词: 延迟环节,burst控制方法,静态工作点,等效仿真模型,瞬态响应
1. 引言
在现代电源芯片设计中,模数结合的方法已经很常见。数字控制的方法的好处是:抗干扰能力强; 控制精确; 灵活性好; 系统的兼容性好; 方便实现电源管理。在数字控制模式中,可以轻松引入延迟环节,让控制更加灵活,高效。这种方法带来的问题是,在引入延迟环节后,在电源工程设计中,最常见的用零极分布来分析电路响应的方法不再适用。引入延迟环节后,通常传递函数用(G(s))来表示,但在真实过程中,τ 的不确定性让分析难度加大。在工程实践中, 仿真的办法,是快速理解与找到解决问题的有效手段。那么如何设定仿真模型可以得到理想的结果就很重要。本文将基于对一种burst控制方法的理解,给出一种在静态工作点作瞬态响应仿真的方法来获得对这类问题的理解与工程解决方法。
2. 一种有延迟环节的burst控制方法
在这种控制方法里,如图一所示,当芯片进入主动BURST 模式后,芯片停止发出驱动脉冲,也就是图中VCS信号没有出现的区间,因为输出电压的下跌,反馈作用的拉电流(一般是光藕的作用)消失,芯片的FB引脚上的电压在内部电流的作用下开始快速上升,直到VFB_BON 信号,并重新唤醒芯片发出驱动脉冲,让下跌中的输出电压回归正常值。
上面的分析过程是一种设计想得到的理想状态。在实际应用中,我们会发现,在输出电容较小,不合理的反馈设计下,FB引脚上的电压快速上升的时间会远大于芯片理想的设计时间,输出电压的跌落幅度变得不可接受。理论上应该消失的从光藕反馈过来的拉电流并不会因为输出电压的跌落马上消失,这将导致,输出电压跌落过多,而且传统经典的适用于线性时不变系统的控制理论,无法很好的解释与解决这个问题。
burst 控制方法如下图

图一:burst 控制方法
3. 常见的控制电路及静态工作点的分析

图二:常见反馈电路
如图二所示,这是一种常见的由TL431 与光藕组成反馈电路,反馈补偿是Ⅱ类补偿电路。输出电压为12V。静态工作点主要是确定两个反馈电容在稳态时的电压值。
首先定义光藕的工作状态: CTR :50%; VF: 1.45V
定义光藕的工作电流:IF: 0.33mA (备注:此电流由芯片工作状态决定)
定义TL431参考脚电压: Vref: 2.5V
定义输出电压:Vout=12V
反馈补偿的电容(C1,C2)上的电压为: Vout-VF-(IF*R5)-Vref
得到反馈补偿的电容(C1,C2)上的电压为: 12V-1.45V-(0.33mA x1k)-2.5V ≈ 8V
由此得到在12V稳态下,C1,C2上的电压为8V
4. 仿真建立方法与等效仿真模型
实际工程样机为一台60W,12V/5A的电源,控制芯片的burst 控制方法如前图一所示
建立的仿真电路如下图三所示。

图三:仿真电路
这种仿真分析方法的目的是用来帮助理解电路的工作与工程实践中的元件参数的调试方向。很明显,流经此二极管的电流会影响电源控制芯片反馈(FB) 脚上电压的上升,控制的目标就是,让这一路电流尽快掉到最小,以得到反馈(FB)电压的上升。
仿真结果如下:
电路的初始参数如图三所示
选取不同的反馈电阻值,如图三中的R2(3k-100k),对流经光藕的电流IPROB2分析,得到图四,图五,不同反馈补偿电阻值下的光藕电流随时间变化规律。
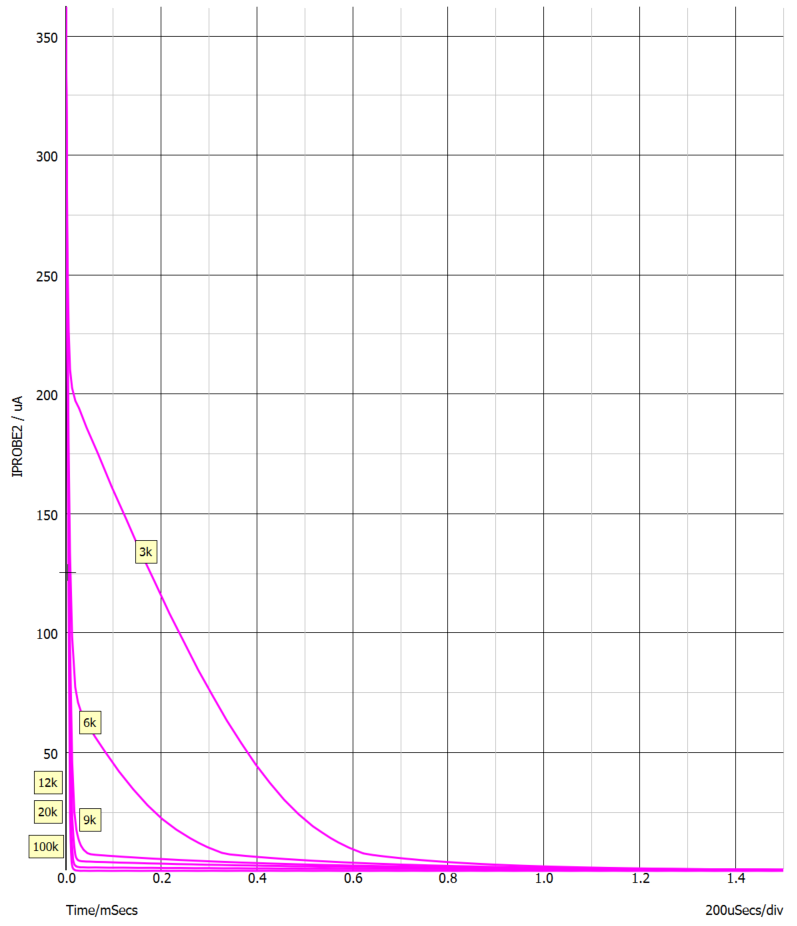
图四:不同反馈补偿电阻值下的光藕电流随时间变化规律
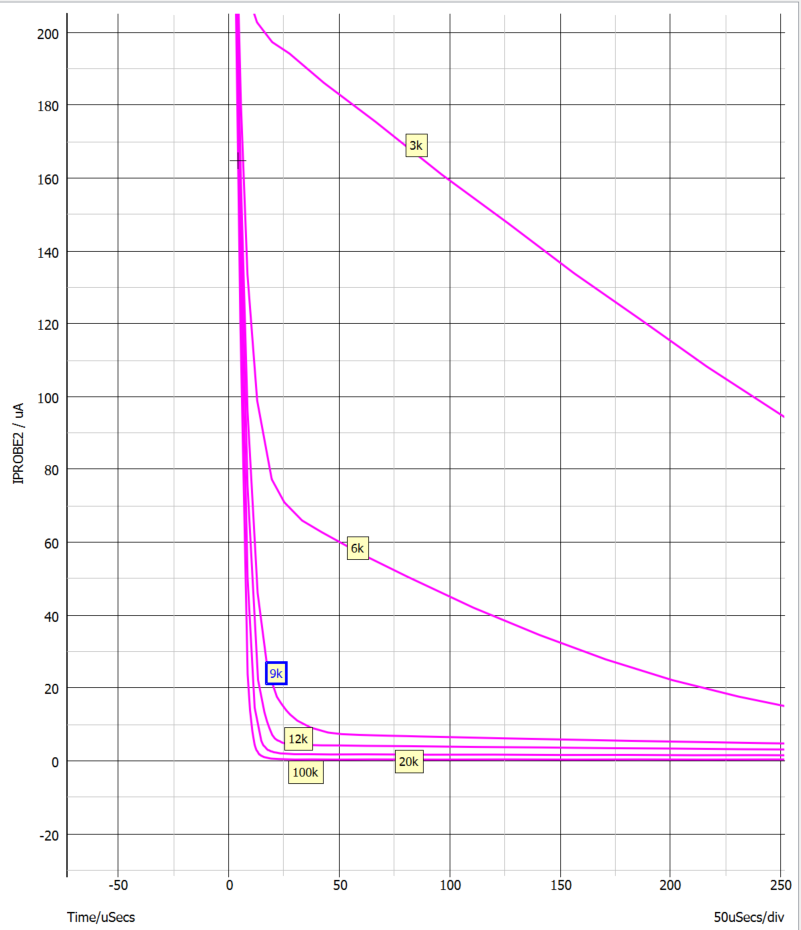
图五:不同反馈补偿电阻值下的光藕电流随时间变化规律(放大版)
选取不同的反馈电容值,图三中的C1(10nF-1uF) ,对流经光藕的电流IPROB2分析,得到图六。
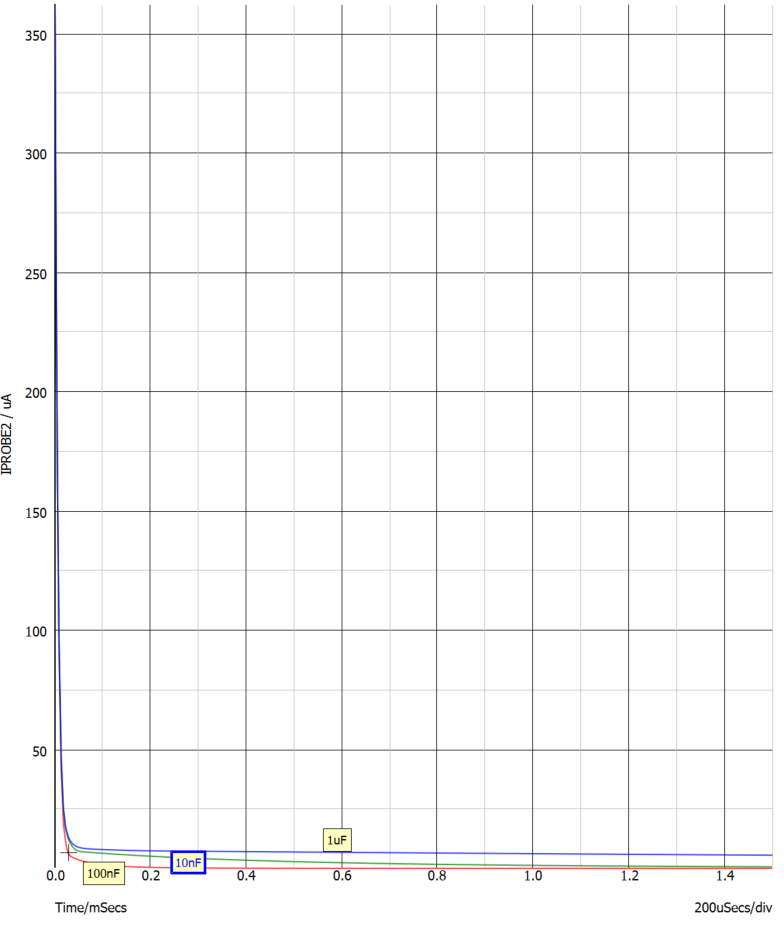
图六:不同反馈补偿电容(C1)值下的光藕电流随时间变化规律
选取不同的反馈电容值,图三中的C2(1nF-100nF),对流经光藕的电流IPROB2分析,得到图七。
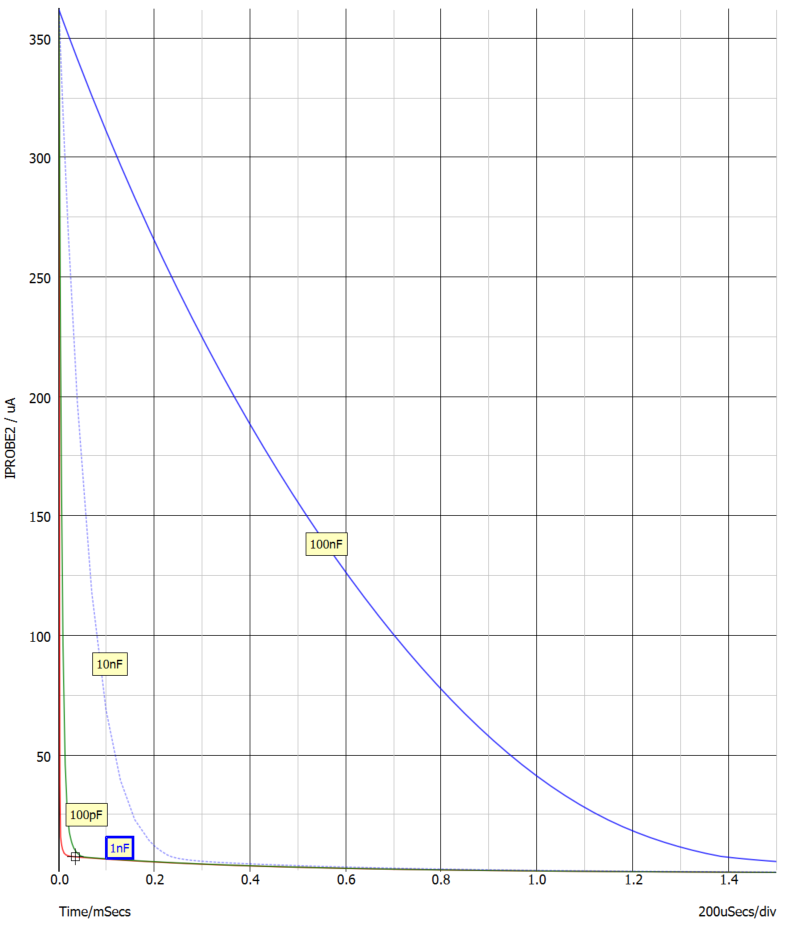
图七:不同反馈补偿电容(C2)值下的光藕电流随时间变化规律
仿真结果分析
从仿真的结果看,环路补偿的三个参数对流过光藕的电流,即同比于FB上升(延时)到重新开启输出驱动的时间,影响很不相同。电阻R2的选择影响很大,超过一定值后,开始收敛,影响开始变化不大。选好较大值的R2 后,与之串联的C1,对结果影响很小。而极点电容C2 ,值选的越大,结果越差。
从理论分析来看,如图三所示,当电源主控芯片停止发驱动, 输出下跌后,TL431的参考电压低于TL431的基准电压2.5V,TL431的阴极电压就会上升,这个上升的电压会通过反馈补偿网络R1,C1,C2补偿TL431的基准电压,如果基准电压被重新抬升到2.5V,TL431会重新导通,产生拉电流,这个电流会有部分流过光藕,影响了流过光藕的电流收敛速度,并与阴极上升的电压建立一定程度的动态平衡。这与仿真的结果是一致的。
实验验证
在实际应用中,C2的值一般都比较小,主要考虑R2 ,C1的影响,为此实验选择了一台60W,输出12V/5A 的电源,按照图三的反馈网络,选取不同参数,测试FB引脚上的电压快速上升的时间(TR),来验证仿真结果。实际测试中,为了得到系统进出Burst的条件,负载设为动态,从1A到0.3A动态变化。波形八到十三的图中,曲线C1为实测的FB 引脚上的电压波形,曲线C2为芯片的驱动波形。
1)选取参数如下:首先定义电容C2的值为1nF,定义电容C1 的值为100nF,选取不同的电阻R2 的值: 3K,9.1K,20K,75K。(结果见图八,图九,图十, 图十一)
2)选取参数如下:首先定义电容C2的值为1nF, 定义R2 的值为75K,选取不同的C1 的值: 1uF,10nF. (结果见图十二,十三)
实际测试结果如下表一和表二
| C2=1nF;C1=100nF | ||||
| R2 | 3K | 9.1K | 20K | 75K |
| TR | 740uS | 582.6uS | 427.8uS | 259uS |
表一: 上升时间随R2 变化表
| C2=1nF; R2=75k | |||
| C1 | 10nF | 100nF | 1uF |
| TR | 250.6uS | 259uS | 276.6uS |
表二: 上升时间随C1的变化表
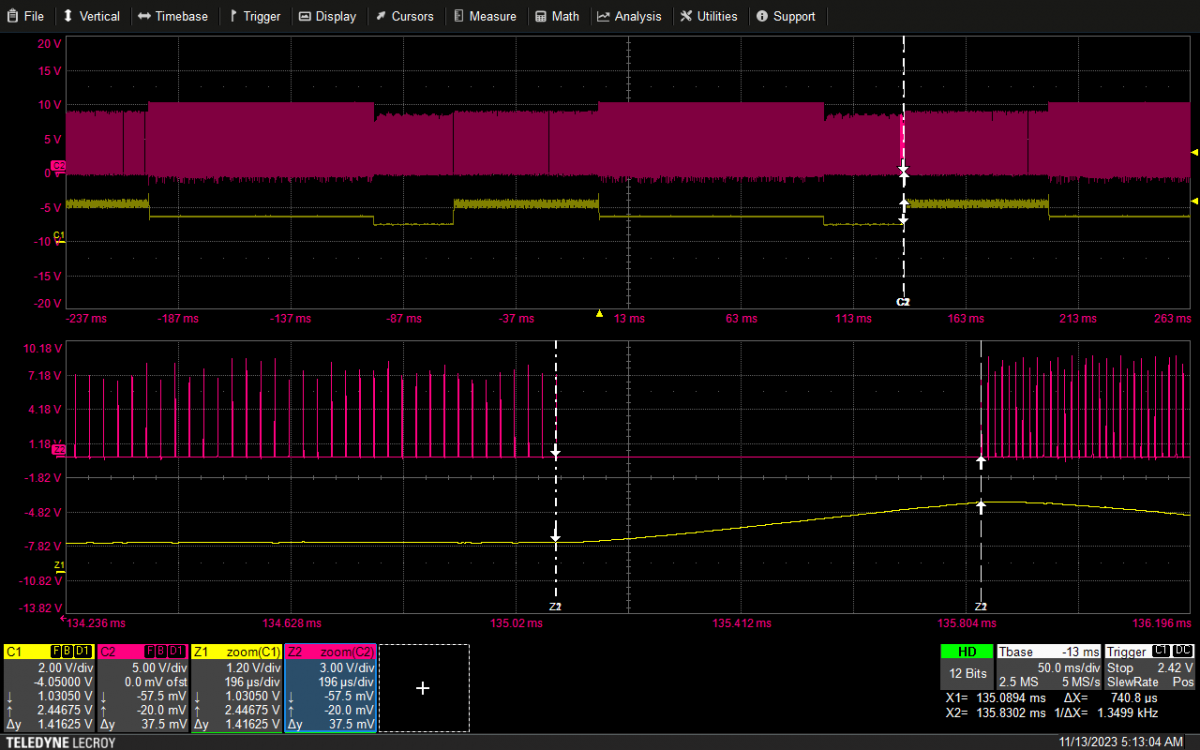
图八:3K/100nF 740Us
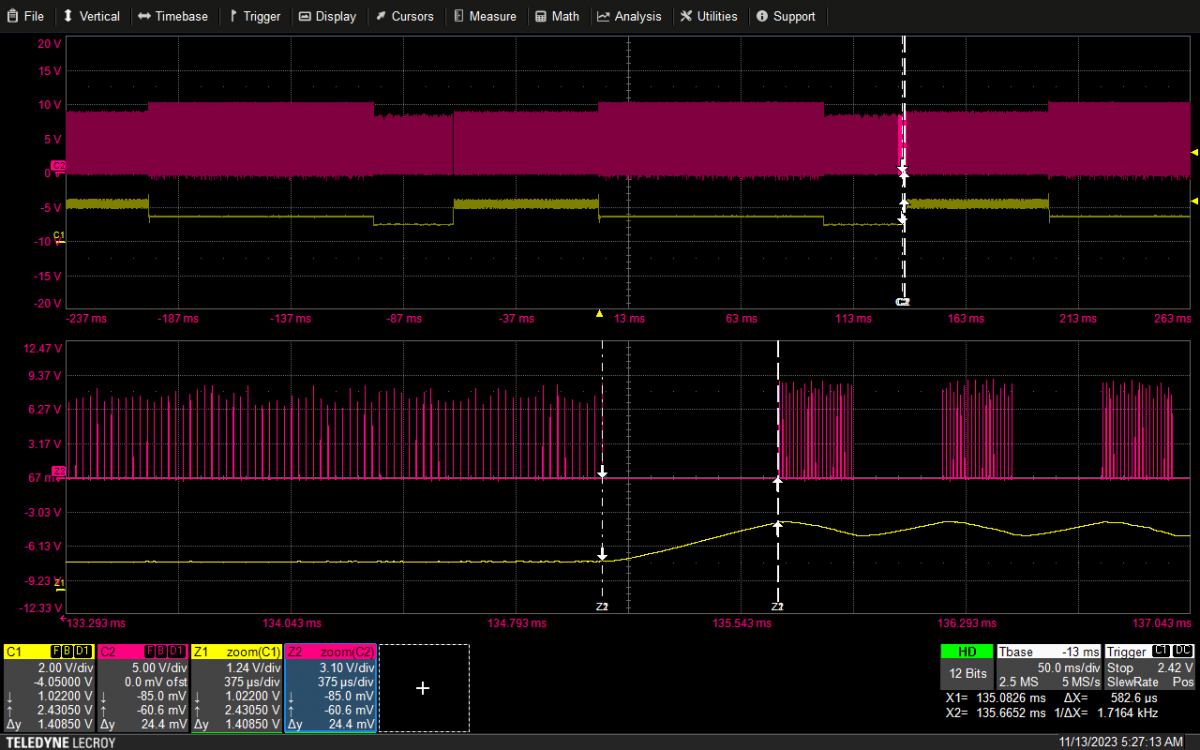
图九:9.1K/100nF 582.6US
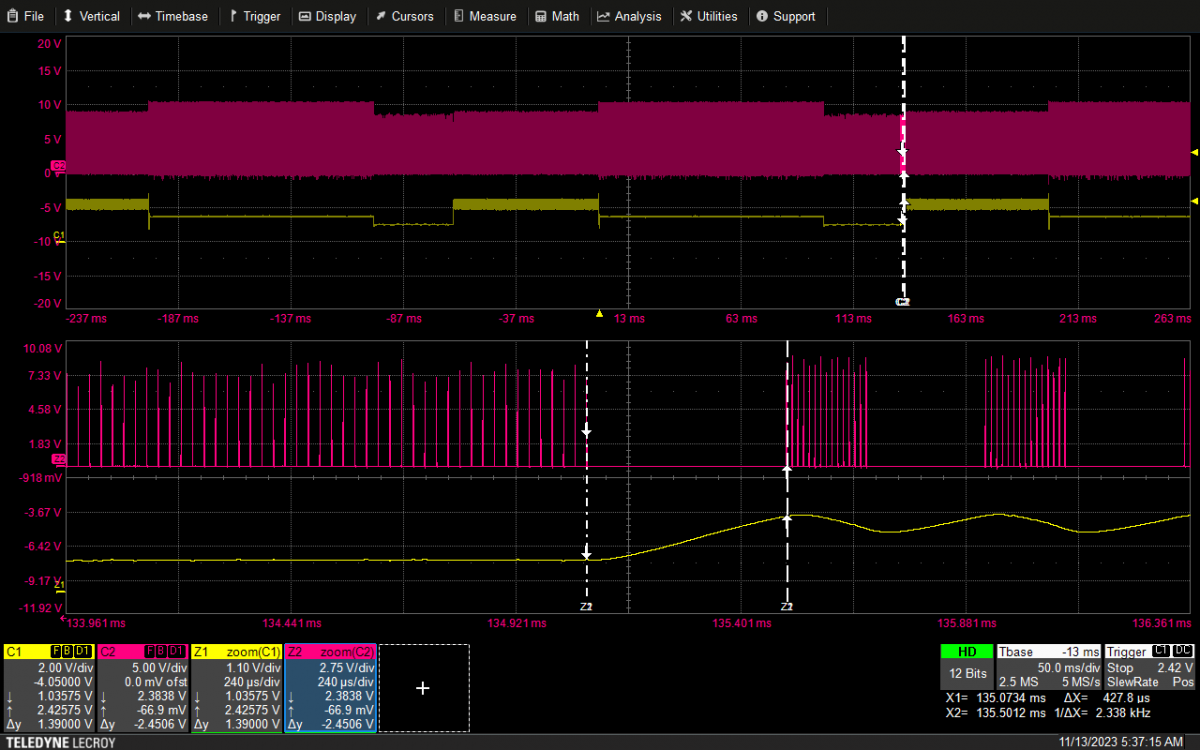
图十:20K/100nF 427.8uS

图十一:75k/100nF 259uS
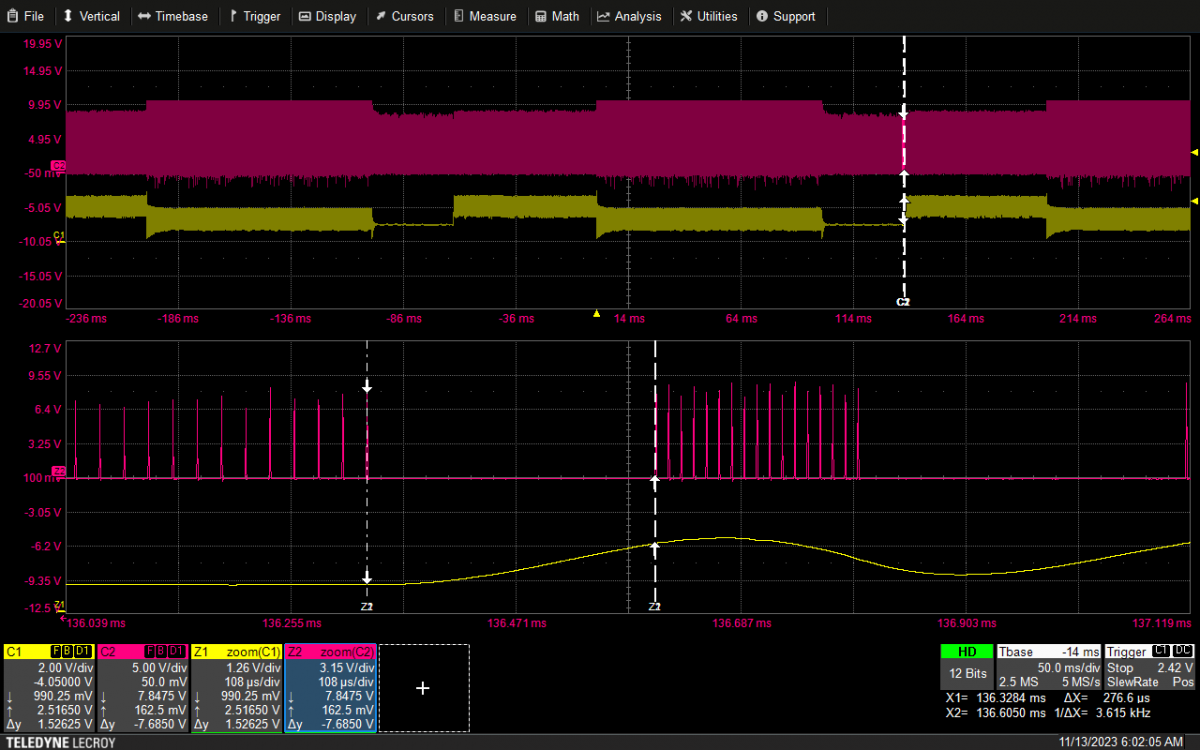
图十二:75K /1uF 276.6uS
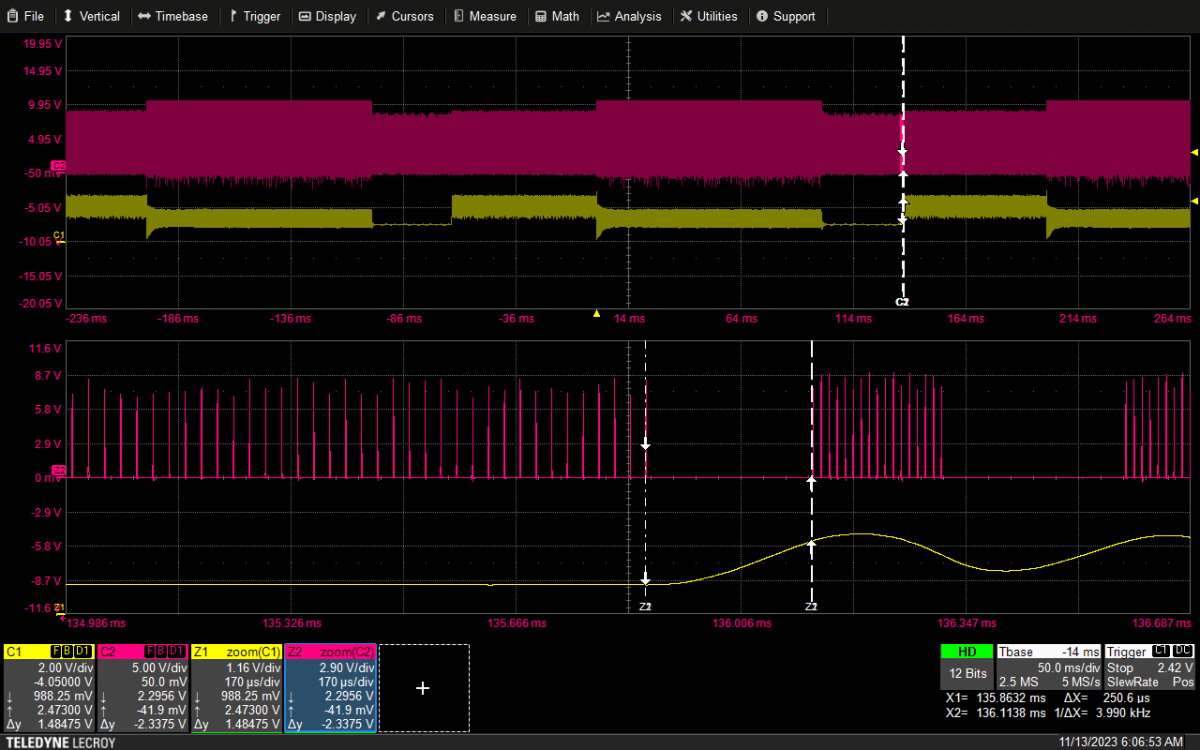
图十三:75K/10nF 250.6uS
结论
从实测的结果来看,反馈电压(FB)的上升时间与仿真的结果,变化的方向完全一致。因而,这种仿真方法能在这种有延迟环节的burst控制方法中得到响应时间的变化规律,在反馈补偿网络中,选择较大的反馈电值,与较小的极点电容,有利于让流过光藕的电流快速收敛至最小值。利用在静态工作点作瞬态响应仿真的方法可以快速得到近似工程解。
参考文献:
ICE5ARXXXBZS 数据表,英飞凌科技股份有限公司
DEMO 5GSAG 60W1演示板,英飞凌科技股份有限公司
Model 310, 0.01 Hz - 30 MHz Frequency Response Analyzer
开关电源环路中的TL431, Christophe Basso
Designing control loops for linear and switching power supplies, Christophe Basso