OPTION_5:HP
简介
现代电子设备在不断小型化,尤其是移动设备现采用多种无线电通信标准,这些都要求对体声波 (BAW) 滤波器技术进行持续的研究和开发。从制造业的角度看,必须处理更小的特性,实现更高的精度,而从设备物理诱发边界的角度来看也是如此,在本文中这一点体现为功率密度限制。高功率密度外加散热能力不足会直接导致设备温度升高。设备温度高又会导致生命周期缩短,故障率上升或零件不满足过温规范。如果只能通过实际零件的首次测量来确认这些缺陷,会浪费大量资源。换言之,如果某种工具能对已处于早期仿真阶段的设计进行热行为预测,且不需要实际硬件,则将大幅提高设计周期的效率。
热仿真的问题是,虽然其背后的物理过程很简单,但由于几何体很复杂,使用分析方法常常不可行。芯片上有多个谐振器,每个散热量均不相同,散热途径多变,散热所通过的倒装芯片支柱采用多种材料并通过硅衬底联通,有时会通过相当复杂的路径,如嵌入层叠绝缘材料的金属轨迹。考虑到这一切,逻辑上来说下一步应该使用有限元建模 (FEM) 仿真。尽管这从一定程度上克服了几何复杂性难题,但又产生了其他问题。滤波器芯片上与温度紧密相关的薄层与系统的其他部分相比,长宽比很高,这使得划分几何体网格更加复杂。这一点可通过不同的网格划分方法来克服。每个谐振器的散热量取决于其在滤波器中的电气行为。因此,对于每个相关频率,电气仿真必须与 FEM 热仿真结合进行。而且,没有直接方法可以仿真由于滤波器的自加热导致的温度诱发性频率偏移。也有资源和可用性方面的考虑。首先,滤波器设计师不需要成为 FEM 专家。他们需要一款简单的工具,能够为他们提供不同方案的相关温度。其次,如果每位用户均需要在自己的计算机上执行 FEM 仿真,软件和许可证成本将非常昂贵,难以接受。此外,设置每次仿真所需的人力成本还需另算。
所有上述原因使得我们得出一个结论,即采用混合仿真是最理想的方法。它将利用两方面的优势:在电路仿真器中使用电热部分来计算各个谐振器由施加信号导致的耗散功率,并根据温度修改谐振器的参数。另外通过 FEM 仿真部分进行补充,它可提供热电阻矩阵,从而给出耗散功率和温升之间的关系。每个设计只需执行一次需要设置且计算量较大的 FEM 仿真((通过现有的用于电磁 FEM 仿真的三维模型自动完成)),后续的针对不同输入功率或输入频率执行的电热仿真与电气仿真相比,仅需一笔较小的开销。只需替换设计中的谐振器模型即可将已有的电气模型转换为电热模型。因此设计师可以轻松地使用工具,这有利于他们从热的角度调整他们的设计。
模型实现
A.电热电路模型
BAW 滤波器仿真的基本结构单元当然是 BAW 谐振器模型。在本文中,此模型基于经过修改的巴特沃斯-范·戴克 (BvD) 电路[1](见图 1)。它包括模拟谐振器中发生的损耗的电阻。例如,电阻 Rs 模拟的是铅和电极损耗,而 Ra 模拟的是基本的声损耗。由于所有损耗最终均会转换为热,因此需要计算所有这些损耗的和,并将其作为耗散功率由模型提供给电路仿真器。对于这些电热仿真,可以利用电气和热仿真控制方程之间已知的相似性。因此基本来说,每个电路仿真器均可用于仿真热网络。表 1 中列出了使用的电气和热属性之间的等价关系。
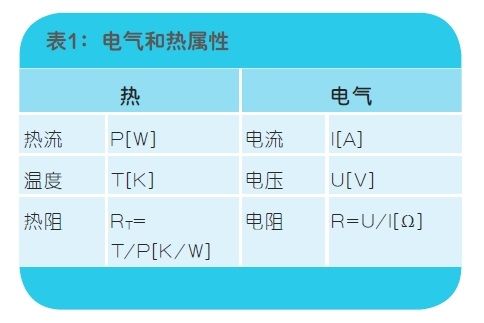
我们的仿真环境提供基本的电热元件,可以将热效应包括在电气仿真中。这些元件包括额外的电热节点。这里我们将聚焦于电阻、电感和电容。对于电阻,此节点将发出电流((单位为安培)),其等价于产生的热流((单位为瓦特))。这三种元件均可根据此节点上检测的电压((等价于温度))更改它们的主要参数,方法是对应于线性、二阶或高阶模型来定义一个或多个温度系数。这些系数定义为各个元件的附加参数。
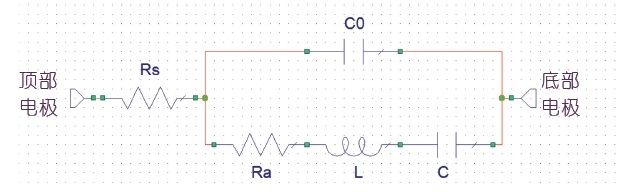
图1.经修改的简单 BvD 谐振器模型。添加了电阻以模拟谐振器损耗。
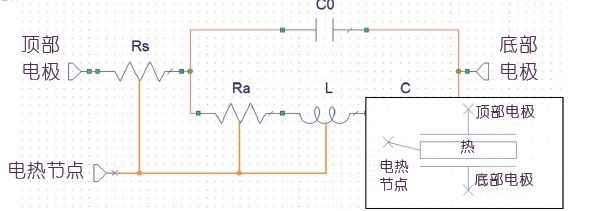
图2.BvD 模型以及电热节点配置的附加示意图。插图:此 BvD 谐振器模型的符号和附加的外部可访问电热节点。
清楚这些以后,现在我们可以基于经修改的 BvD 模型来建立电热谐振器模型,但需要外加电热元件。模型中所有电阻的电热节点均连接到一个公共节点,如电感的电热节点那样(示意图如图2所示)。此公共节点可从谐振器模型的外部进行访问(图2中的插图)。流出此节点的电流代表全部耗散功率,而电压是谐振器的温度。由于电感和公共节点相连,因此我们可以根据温度使用它更改谐振器模型的共振频率。通常对于新的谐振器堆栈,我们已知的温度相关参数是串联共振的频率温度系数 (TCF),因此我们需要一种方法将其转换为 BvD 模型中电感的变化。LC 电路的频率和其元件值之间的已知关系是:

从公式 (2) 和 (4) 可以明显看出,电感的温度系数需要为-2˙TCf。由于 TCf 为30ppm/℃时,△T≤100K,因此此近似导致算得的频率偏移误差低于0.002%。通过TCf计算电感的温度系数是在模型中完成的,因此TCf是必须提供给电热BvD模型的唯一附加项。对于电热自加热仿真,需要使用仿真器来计算模型节点上的电压和电流,因为只能通过此方法推导出功率耗散。标准 RF 仿真仅求解阻抗网络,不需要电压和电流,因此也无法计算耗散功率。
最后需要的一项是热阻,它可以将耗散功率和模型谐振器的温度关联起来。由于目标是仿真在单个芯片上包含多个谐振器的滤波器,因此热环境将不仅仅是到各个谐振器热接地的单个热电阻。即使是这种情况,但由于滤波器模块的几何体非常复杂,计算各个值也将不切实际。由于谐振器之间会发生交叉加热(主要是衬底引起的热交换),因此各个谐振器之间必定有热电阻。因此需要整个热电阻矩阵。
B. FEM仿真
为了计算所有谐振器之间和到热接地的热阻,将执行以下步骤。通过已知功率加热一个谐振器。计算温度分布,将所有谐振器的平均温度值保存在矢量中。图3给出了此类仿真温度场的示例。然后单独加热下一个谐振器,并保存所有谐振器温度。通过此方法对所有谐振器执行操作后,我们将得到一个 n*n 矩阵,其中 n 为仿真中的振荡器数量。接着,此温度矩阵需要除以对角矩阵,后者由用于在仿真中加热谐振器的功率所填充,得到热阻矩阵。得到的矩阵当然是对称的,因为两点之间的热阻并不是定向的。此过程可以自动执行以提高效率。常规的设计流程已经为要研究的滤波器模块提供了自动生成的三维模型。脚本将自动执行以下步骤:
●将三维模型导入 FEM 软件
●删除热 FEM 仿真不需要的几何体,例如某些金属层
●执行基本几何体清理
●准备几何体以实现高效网格化分
●分配材料
●定义并生成网格
●设置物理及边界条件
●设置求解器
●执行上文所述的加热和测量谐振器循环操作
●将得到的热阻矩阵写到标准文件中
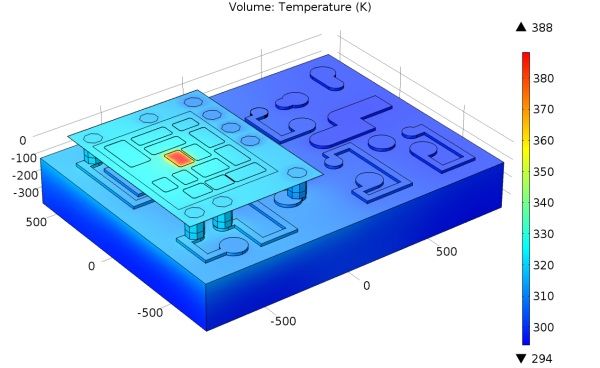
图3.通过FEM仿真得到的某个受热谐振器的温度场(芯片的硅衬底和模块的塑料包塑已隐藏)。
几何体的网格化分包含两种不同的方法,即获得不同零件的正确网格尺寸,同时避免在不必要的位置采用过多的网格单元。设置边界条件时,要考虑的问题是功率耗散到了堆栈中的什么位置。由于绝大多数声能包含在压电层中,因此该处的耗散应该最高,假设粘滞损耗系数在不同材料中不会变化几个数量级以补偿变化的能量。因此,仿真将压电层设置为热源。由于另一种损耗机制,电极中的欧姆损耗,是在压电层下方和上方直接发生,因此从这个角度来说,这种设置也很合理。仿真的输出文件是包含电阻值的 n 端口标准文件。使用标准格式的优势是其可以直接导入任何虚拟的 RF 电路仿真器。
C 最终的仿真设置
有了这两个要素后,即电热 BvD 模型和热阻矩阵,我们可以转换标准电气仿真以纳入热效应。为此,将滤波器示意图中的所有标准谐振器更换为电热模型,将热阻矩阵导入仿真器。然后将谐振器的电热节点连接到热阻矩阵的相应端口(相关示意图见图4)。我们通常使用两种仿真方法来显示不同的信息。在第一种方案中,我们扫描经过滤波器的功率信号并记录电压,从而得到电热节点的温度。这样设计师可以了解设计中的哪个谐振器温度最高以及相应的频率是多少。如果温度过高,设计师可以采取相应的对策。但大多数情况下采用第二种方案,在特定频率下输入一个功率信号,通过小信号 s 参数扫描捕捉通带位置和形状的偏移。这显示了滤波器的自加热将如何影响其性能。由于我们还可以测量各个谐振器的电热节点的耗散功率,因此也可将此信息反馈给 FEM 仿真。例如,如果完全不清楚某个谐振器为什么比其他谐振器的温度高出很多,我们可以查看得到的温度场,研究通过薄层的散热路径。
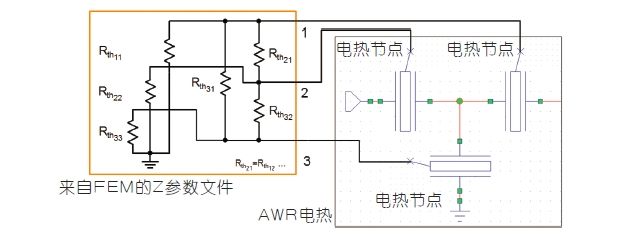
图4.电热谐振器滤波器模型到热电阻矩阵连接的示意图。
结果
本部分给出的仿真使用的是 B7 TX 滤波器,其带宽范围为 2500MHz 到 2570MHz。图 5a 和图 5b 分别给出了施加可扫描的功率信号后,滤波器中包含的各个串联谐振器的温度和热通量随频率的变化。当然,也可以为并联谐振器绘制类似的图(此处未显示)。一个有趣的结果是,即使一些谐振器的通量非常小(红色轨迹),由于周围谐振器的交叉加热,它们的温度也会上升到几乎与具有大量功率耗散的谐振器(黑色、绿色...轨迹)一样高的温度等级。但是也可以看到逆效果。橙色和紫色轨迹显示,最高热通量出现在上频带边沿以上。但是,它们的热接地相当良好,因此温升低于下频带边沿以下的所有谐振器的温升。此示例说明,如果仅考虑功率耗散,得到的结论误导性很高。图 6 给出了第二种仿真方案。在特定频率下施加 CW 信号(此情况中为 30dBm@2.5GHz)以加热滤波器并执行小信号 s 参数扫描以查看得到的带移。在此示例中,信号为 -20dBm 时滤波器的偏移为 -1.4MHz。还可以看出,上频带边沿偏移较小。
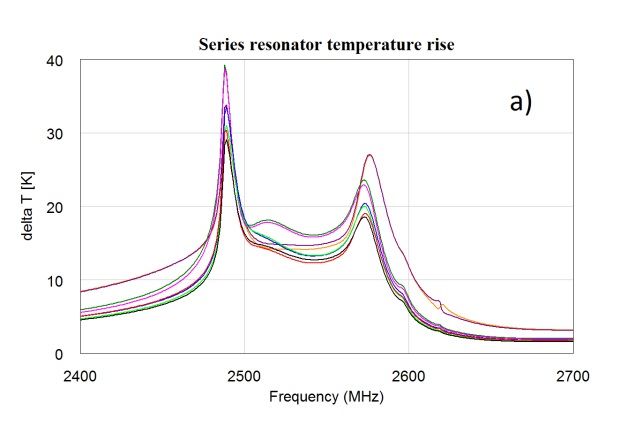
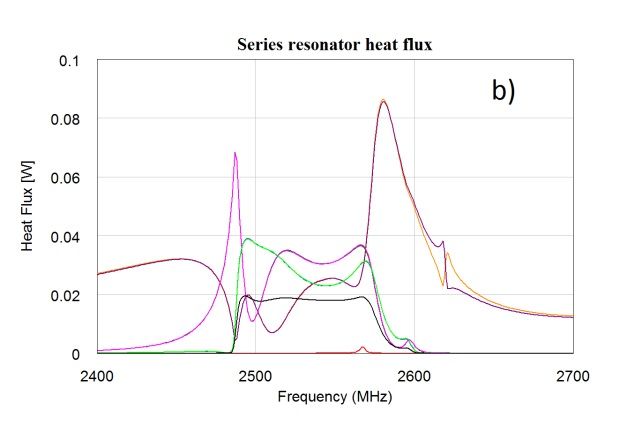
图5.扫描的功率信号方案。显示了八个串联谐振器(不同颜色)
a) 高出环境温度的温升。b) 谐振器耗散的热通量。
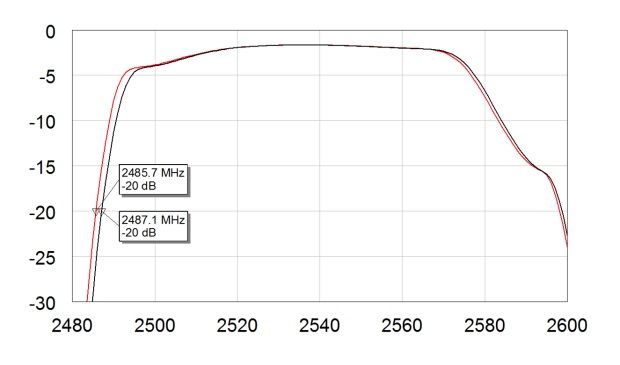
图6.自加热导致的带移。灰色轨迹为小信号 s 参数基线。红色轨迹在 .5GHz 处被施加了功率为 30dBm 的 CW 信号。得到的偏移
结论
我们为 WLP-BAW 滤波器模块的热仿真提供了一种可行的解决方案。这种方案结合了电路仿真器中电热仿真的简单性与速度以及捕捉复杂几何体(如薄层)影响的 FEM 仿真的能力。通过自动执行所有相关设置和仿真步骤,巧妙解决了需要处理 FEM 仿真的问题。因此,我们为滤波器设计提供了一款简单而强大的工具。
参考文献
[1] W. P. Mason, Ed., “Physical acoustics: principles and methods” Academic Press, New York, vol. 1 part A, pp. 233ff, 1964.
本文来自《电子工程专辑》2016年3月《微波及射频》特刊,拒绝转载。