RFI整流原理阐释

输入级RFI整流灵敏度

模拟集成电路中有一种众所周知却又了解不深的现象，即RFI整流，在运算放大器和仪表放大器中尤为常见。放大极小信号时，这些器件可以对大幅度带外HF信号进行整流，即RFI。因此，除所需信号外，输出端还会出现直流误差。不需要的HF信号可以通过多种途径进入敏感模拟电路。引入和引出电路的导体为进入电路的干扰耦合提供了通路。这些导体会通过容性、感性或辐射耦合拾取噪声。杂散信号会和所需信号一起出现在放大器输入端。杂散信号的幅度虽然可能只有几十毫伏，但是也会产生一些问题。简言之，敏感低带宽直流放大器未必总能抑制带外杂散信号。对简单的线性低通滤波器而言，情况确实如此，而运算放大器和仪表放大器实际上会对高电平HF信号进行整流，从而导致非线性和异常失调。本指南将讨论RFI整流的分析和预防方法。

背景知识：运算放大器和仪表放大器RFI整流灵敏度测试

几乎所有的仪表放大器和运算放大器输入级都采用某种类型的射极耦合BJT或源极耦合FET差分对。根据器件工作电流、干扰频率及其相对幅度，这些差分对可以像高频检波器一样工作。检波过程会在干扰的谐波频谱成分上产生噪声，同样也会在直流分量上产生噪声！从干扰中检测到的直流成分会转换放大器偏置电平，导致结果不准确。

运算放大器和仪表放大器中的RFI整流效果可以通过相对简单的测试电路来评估，如RFI整流测试配置中所述。在这些测试中，运算放大器或仪表放大器增益配置为–100(运算放大器)或100(仪表放大器)，直流输出在100 Hz低通滤波器后测量，以防来自其它信号的干扰。测试激励选用100 MHz、20 mVp-p信号，远高于测试器件的频率限制。操作时，测试可以评估存在激励时观察到的直流输出偏移。该测量的理想直流偏移为零，给定器件的实际直流偏移表示相对RFI整流灵敏度。采用BJT和FET技术的器件都可以通过该方法来测试，因为这些器件在高低电源电流水平下都可以工作。

在原始运算放大器测试中，有些FET输入器件的输出电压不具有可观察的偏移，而其它有些器件则表现出小于10 μV的偏移(折合到输入端)。在BJT输入运算放大器中，偏移量会随着器件电源电流的增加而减小。只有两款器件不具有可观察的输出电压偏移，其它器件的偏移则小于10 μV(折合至输入端)。可想而知，其它运算放大器在接受此类测试时也会表

现出类似模式。

通过这些测试，可以概括出RFI整流的一些特点。首先，器件耐受性似乎与电源电流成反比，也就是说，在低静态电源电流下偏置的器件具有最高的输出电压偏移。其次，具有FET输入级的IC似乎比具有BJT的IC不易受整流影响。注意，无论是运算放大器还是仪表放大器，这些特点都是独立的。实际上，这意味着低功耗运算放大器或仪表放大器更易受RFI整流影响。而且，FET输入运算放大器(或仪表放大器)更不易受RFI整流的影响，在较高电流下工作时尤为如此。

根据上述数据和BJT与FET的基本差异，我们可以总结一下之前了解的内容。双极性晶体管效应受正偏PN结(基极-发射极结)的控制，该结点的I-V特性具有指数特性和明显的非线性。另一方面，FET特性受施加到反向偏置PN结二极管上电压的控制(栅极-源极结)。FET的I-V特性满足平方律，因此，本身就比BJT更具有线性。

对低电源电流器件而言，电路中的晶体管经过偏置后，电流远低于其峰值fT集电极电流。虽然IC构建所用的工艺涉及的器件fT可达几百MHz，但是晶体管在低电流水平下工作时，电荷跃迁时间会增加。采用的阻抗水平也使这些器件中的RFI整流变得更差。在低功耗运算放大器中，阻抗约为几百到几千千欧，而在中等电源电流设计中，阻抗可能不超过几千欧。在这些因素的共同作用下，低功耗器件的RFI整流特性变差。

图1总结了关于RFI整流灵敏度的一般性观察，运算放大器和仪表放大器均适用。

图1：关于运算放大器和仪表放大器输入级RFI整流灵敏度的一些一般性观察

点击下一页：分析方法：BJT RFI整流

{pagination}

分析方法：BJT RFI整流

实验表明，与具有FET输入的类似器件相比，BJT输入器件具有更高的RFI整流灵敏度，可以采用分析性更强的方法来解释这一现象。

RF电路设计人员早就知道，由于具备非线性I-V特性，PN结二极管是有效的整流器。HF正弦波输入的BJT晶体管电流输出频谱分析表明，器件偏置越接近“膝部”，非线性就越高。这会进而使其用作检波器时更为有效。这一点在低功耗运算放大器中尤为重要，此时输入晶体管在极低集电极电流时会发生偏置。

参考文献1中说明了BJT集电极电流的整流分析方法，在此恕不赘述，除非需要作出重要结论。这些结果表明，原始二次二阶项可以简化为频率相关项△i_c(AC)(两倍输入频率下)和直流项△i_c(DC)。后一项可以采用公式2表示，整流直流项的最终形式为：

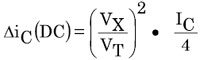
   公式1

该公式表明，二阶项的直流成分与HF噪声幅度V_X的平方以及晶体管的静态集电极电流I_C成正比。为了表明整流的这一特点，注意，在I_C为1 mA条件下工作、具有10 mVpeak高频信号冲击的双极性晶体管的直流集电极电流变化约为38μA。

减少整流集电极电流需要减少静态电流或干扰幅度。由于运算放大器和仪表放大器输入级很少提供可调整静态集电极电流，迄今为止，减少干扰噪声V_X水平还是最佳(也几乎是唯一)解决方案。例如，将干扰幅度减少2倍至5 mV_peak后，会使整流集电极电流产生4到1的净减少量。显然，这说明必须使杂散HF信号远离RFI敏感放大器输入端。

分析方法：FET RFI整流

参考文献1中也说明了JFET漏极电流的整流分析方法，在此恕不赘述。类似的方法也用于FET漏极电流整流分析，该电流与施加到其栅极的小电压V_X成函数关系。公式2概括了FET漏极电流二阶整流项的评估结果。和BJT一样，FET二阶项也有交流和直流成分。此处给出了整流漏极电流直流项的简化公式，其中整流直流漏极电流与杂散信号，即V_X幅度的平方成正比。

但是，公式2也说明，由FET和BJT产生的整流度的差异非常重要。

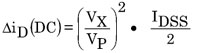
   公式 2

但是，在BJT中，集电极电流的变化与其静态集电极电流水平存在直接关系，JFET漏极电流的变化与处于零栅极-源极电压的漏极电流I_DSS成正比，与其通道夹断电压V_P的平方成反比，参数为几何参数，取决于过程。通常,用于仪表放大器和运算放大器输入级的JFET偏置时的静态电流约0.5·I_DSS。因此,JFET漏极电流的变化与其静态漏极电流无关,所以也和工作点无关。

图2所示为BJT和FET之间二阶整流直流项的定量比较。本例中，双极性晶体管具有576μm2的单位发射面积，相对于用于20μA IDSS和2 V夹断电压的单位面积JFET。每个器件都在10μA条件下偏置，工作温度T_A = 25℃。

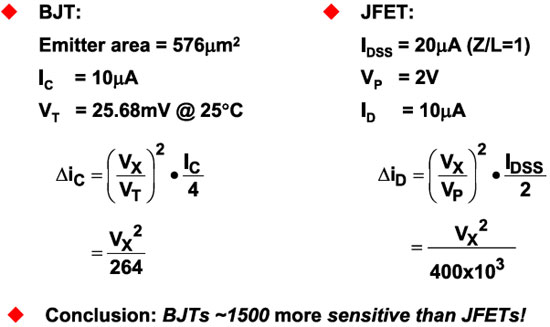
图2：BJT与JFET相对灵敏度比较

在相同的静态电流水平下，双极性晶体管中集电极电流的变化比JFET漏极电流的变化约大1500倍，这一结论非常重要。这就可以解释为什么FET输入放大器表现出的灵敏度小于大幅度HF激励。因此，它们可以提供更多RFI整流抗扰度。

根据上述内容，可以作出如下总结：由于用户几乎无法查看放大器的内部电路，防止因RFI导致IC电路性能下降对IC外部电路而言就显得尤为重要。

上述分析表明，无论采用哪种类型的放大器，RFI整流都与干扰信号幅度的平方成正比。因此，为了尽可能减少精密放大器中的RFI整流，必须在输入级之前减少或消除干扰电平。减少或消除干扰噪声的最直接方法是适当滤波。

点击下一页：减少运算放大器和仪表放大器电路中的RFI整流

{pagination}

减少运算放大器和仪表放大器电路中的RFI整流

EMI和RFI会严重影响高精度模拟电路的直流性能。由于带宽相对较低，精密运算放大器和仪表放大器不会精确放大MHz范围内的RF信号。但是，如果这些带外信号能够通过精密放大器的输入、输出或电源引脚耦合至精密放大器，这些信号就会通过各种放大器结点进行内部整流，并最终在输出端导致不必要的直流失调。之前关于该现象的理论探讨已经说明其基本机制。下一步要介绍合适的滤波如何减少或消除这些误差。

合适的电源去耦可以将IC电源引脚上的RFI降至最低。放大器输入和输出还需要在器件级进一步探讨。此时，假定系统级EMI/RFI方法已经实现，如紧凑的RFI外形、正确接地的屏蔽层、电源轨滤波等。这些后续步骤可视为电路级EMI/RFI防护。

运算放大器输入

防止输入级整流的最佳方法是采用靠近运算放大器输入的低通滤波器，如图3所示。

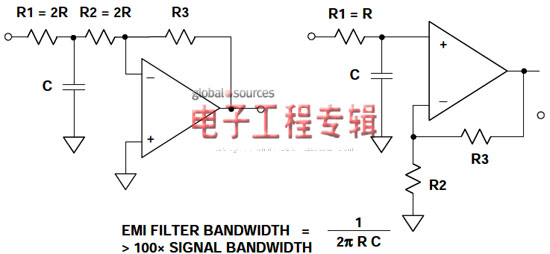
图3：用于运算放大器电路的简单EMI/RFI噪声滤波器

在左侧示意图的反相运算放大器中，滤波器电容C位于等值电阻R1-R2之间。由此可以得出简单的转折频率表达式，如图所示。在极低频率或直流情况下，电路的闭环增益为–R3/(R1+R2)。注意，C不能直接连接至运算放大器的反相输入，否则会产生不稳定性。所选的滤波器带宽至少为信号带宽的100倍，以便将信号损失降至最低。

在右侧示意图的同相运算放大器中，电容C可以直接连接至运算放大器输入，阻值为“R”的输入电阻会和反相运算放大器产生相同的转折频率。两种情况下都应采用低电感芯片式电容，如NP0陶瓷电容。电容在任何情况下都不应出现损耗或电压系数问题，因此只能选用上述NP0陶瓷电容或薄膜型电容。

需要注意的是，可以用铁氧体磁珠代替R1，但是，铁氧体磁珠阻抗无法精确控制，一般不超过100Ω(10 MHz至100 MHz时)。因此，需要采用容值较大的电容来衰减低频。

点击下一页：仪表放大器输入

{pagination}

仪表放大器输入

由于存在共模(CM)EMI/RFI，精密仪表放大器对直流失调误差尤为敏感。这和运算放大器中存在的问题很像。而且，和运算放大器相比，采用低功耗仪表放大器时，EMI/RFI灵敏度问题尤为严重。

图4所示为仪表放大器器件级应用正确的通用滤波方法。实际上，该电路中的仪表放大器可以采用各种器件中的任何一种。仪表放大器之前相对复杂的平衡RC滤波器可以处理所有的高频滤波。仪表放大器可以通过其增益设置电阻，针对应用所需的增益进行编程(图中未显示)。

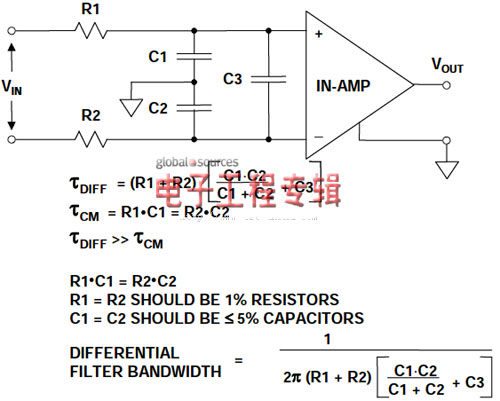
图4：仪表放大器通用共模/差模RC EMI/RFI滤波器

注意，在滤波器中，共模(R1-C1和R2-C2)和差模(DM)信号(R1+R2，以及C3 || 串联的C1-C2)均受到完全平衡的滤波。如果R1-R2和C1-C2匹配不佳，V_IN的部分输入共模信号就会转换为仪表放大器输入端的差模信号。因此，C1和C2相互间至少有5%匹配。R1和R2应为1%金属薄膜电阻，以利于匹配。假定从V_IN端获得的源阻抗相对R1-R2较低，且能够匹配。在这种滤波器中，所选的C3应远大于C1或C2(C3≥C1、C2)，以便抑制由于R1-C1和R2-C2时间常数不匹配引起共模(CM)-差模(DM)转换，从而导致的杂散差分信号。

整体滤波器带宽应至少为输入信号带宽的100倍。实际上，滤波器元件应对称安装在具有大面积接地层的PC电路板上，而且必须靠近仪表放大器输入端，以便实现最佳性能。

图5所示为该滤波器系列，适合各种不同的仪表放大器。RC元件应按照表中要求，根据不同的仪表放大器量身定制。选择这些滤波器元件是为了使低EMI/RFI灵敏度和低噪声增加量达到适度平衡(与无滤波器的相关仪表放大器相比)。

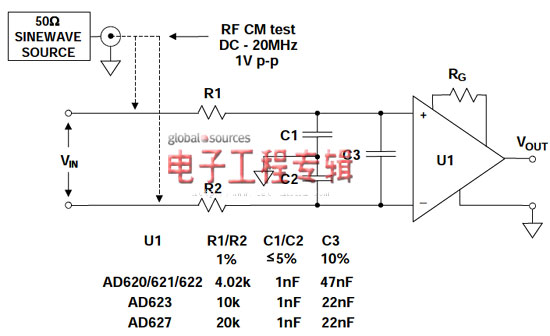
图5：适用于AD620系列、AD623、AD627和其它仪表放大器的灵活共模和差模RC EMI/RFI滤波器

为了测试配置的EMI/RFI灵敏度，可以向输入电阻施加1 Vp-p的共模信号，如图所示。采用常用的仪表放大器(如AD620)，在增益为1000的条件下工作时，获得的最大RTI输入失调电压偏移在20 MHz范围内为1.5μV。在AD620滤波器示例中，差分带宽约为400 Hz。

共模扼流圈提供简单的单器件EMI/RFI保护，可以替代无源RC滤波器，如图6所示。

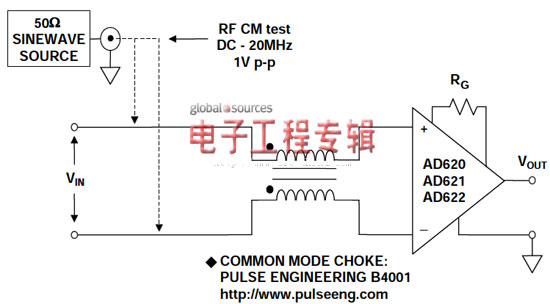
图6：为简明起见，以及实现最低噪声EMI/RFI滤波操作，共模扼流圈适用于AD620系列仪表放大器

除了采用的元件数量较少以外，通过电阻的消除作用，基于扼流圈的滤波器还具有低噪声。但是，选择合适的共模扼流圈至关重要。图6所示电路中采用的扼流圈是Pulse Engineering B4001。从DC至20 MHz(G = 1000)测得的最大RTI失调偏移为4.5μV。可以采用现成的扼流圈(如B4001)，也可以另行制造。绕组的平衡非常重要，因此，建议采用双线绕组。当然，磁芯材料必须能够在预期频带内工作。注意，和图5中的RC滤波器系列不同，只采用扼流圈的滤波器无法提供差分滤波。通过增加图5所示的R1-C3-R2连接，可以在扼流圈后采用第二级设置选择增加差模滤波。

放大器输出和EMI/RFI

除了对输入和电源引脚进行滤波外，还需要防止放大器输出受到EMI/RFI的影响，在需要驱动用作天线的较长电缆时尤其必须注意。从输出线路收到的RF信号可以耦合回其受到整流的放大器输入端，并以失调偏移的形式再次出现在输出端。

电阻和/或铁氧体磁珠(或两者)与输出串联后，即构成最简单廉价的输出滤波器，如图7(上方电路)所示。

增加图7所示的电阻-电容-电阻“T”型电路(下方电路)后，可以改进该滤波器，只会略微变得复杂一些。输出电阻和电容会使大部分高频能量移出放大器，使该配置即使在低功耗有源器件中也同样适用。当然，必须仔细选择滤波器元件的时间常数，将所需输出信号下降程度降至最低。

本例中，所选的RC元件约为3 MHz信号带宽，适用于仪器仪表或其他低带宽级应用。

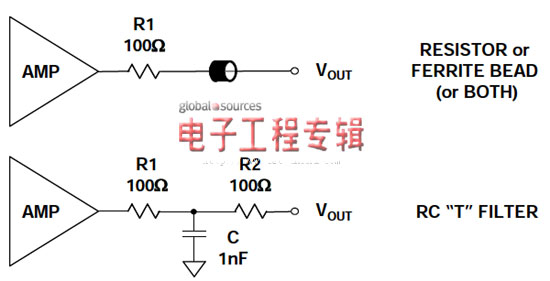
图7：应防止运算放大器和仪表放大器输出受到EMI/RFI的影响，尤其在驱动长电缆的情况下

参考文献：

1. James Wong, Joe Buxton, Adolfo Garcia, James Bryant, "Filtering and Protection Against EMI/RFI" and "Input Stage RFI Rectification Sensitivity", Chapter 1, pg. 21-55 of Systems Application Guide, 1993,Analog Devices, Inc., Norwood, MA, ISBN 0-916550-13-3.

2. Adolfo Garcia, "EMI/RFI Considerations", Chapter 7, pg 69-88 of High Speed Design Techniques, 1996,Analog Devices, Inc., Norwood, MA, 1993, ISBN 0-916550-17-6.

3. Walt Kester, Walt Jung, Chuck Kitchen, "Preventing RFI Rectification", Chapter 10, pg 10.39-10.43 of Practical Design Techniques for Sensor Signal Conditioning, Analog Devices, Inc., Norwood, MA, 1999,ISBN 0-916550-20-6.

4. Charles Kitchin and Lew Counts, A Designer's Guide to Instrumentation Amplifiers, 3rd Edition, Analog Devices, 2006.

5. B4001 and B4003 common-mode chokes, Pulse Engineering, Inc., 12220 World Trade Drive, San Diego,CA, 92128, 619-674-8100, http://www.pulseeng.com

6. Understanding Common Mode Noise, Pulse Engineering, Inc., 12220 World Trade Drive, San Diego, CA,92128, 619-674-8100, http://www.pulseeng.com

7. Hank Zumbahlen, Basic Linear Design, Analog Devices, 2006, ISBN: 0-915550-28-1. Also available as Linear Circuit Design Handbook, Elsevier-Newnes, 2008, ISBN-10: 0750687037, ISBN-13: 978-0750687034. Chapter 12

8. Walt Kester, Analog-Digital Conversion, Analog Devices, 2004, ISBN 0-916550-27-3, Chapter 9. Also available as The Data Conversion Handbook, Elsevier/Newnes, 2005, ISBN 0-7506-7841-0, Chapter 9.

9. Walter G. Jung, Op Amp Applications, Analog Devices, 2002, ISBN 0-916550-26-5, Chapter 7. Also available as Op Amp Applications Handbook, Elsevier/Newnes, 2005, ISBN 0-7506-7844-5. Chapter 7.